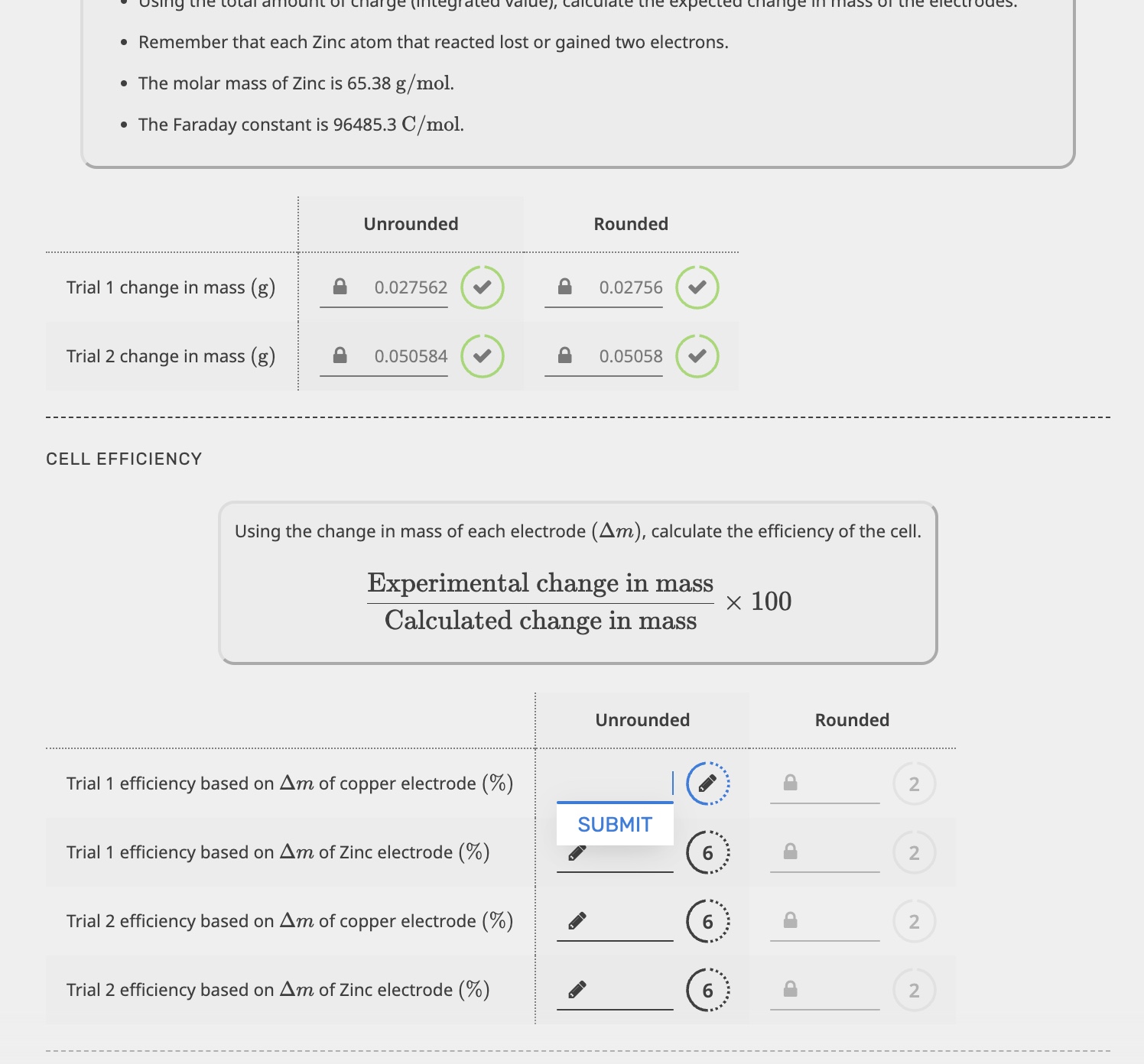
Calculate the cell efficiency for the given trials based on the change in mass of copper and zinc electrodes, using the provided formula and constants.

Steps to Solve

1. Calculate the charge (Q) for each trial. Since the change in mass is due to the transfer of electrons, we need to find the total charge transferred. We know that the change in mass is related to the number of moles of electrons transferred. Rearranging the formula that relates moles, faraday's constant and charge will define the total charge transferred for each trial, where $n$ is the number of moles of electrons transferred and $F$ is Faraday's constant: $Q = nF$ Since we are given the Faraday constant, we need to find the the number of moles exchanged using the change in mass for each trial.

2. Calculate the moles of Zinc for each trial To calculate the number of moles of zinc, we will divide the change in mass of zinc by the molar mass of zinc. For trial 1: $moles_{Zn, trial1} = \frac{0.027562 \ g}{65.38 \ g/mol} = 0.0004216 \ mol$ For trial 2: $moles_{Zn, trial2} = \frac{0.050584 \ g}{65.38 \ g/mol} = 0.0007737 \ mol$

3. Calculate the moles of electrons transferred for each Trial Since each zinc atom loses two electrons ($Zn \rightarrow Zn^{2+} + 2e^-$), the number of moles of electrons transferred is twice the number of moles of zinc. For trial 1: $moles_{e^-, trial1} = 2 \cdot 0.0004216 \ mol = 0.0008432 \ mol$ For trial 2: $moles_{e^-, trial2} = 2 \cdot 0.0007737 \ mol = 0.0015474 \ mol$

4. Calculate the total charge transferred for each trial. Using the formula $Q = nF$ where $n$ is the number of moles of electrons transferred and $F$ is the Faraday constant ($96485.3 \ C/mol$): For trial 1: $Q_1 = (0.0008432 \ mol) \cdot (96485.3 \ C/mol) = 81.35 \ C$ For trial 2: $Q_2 = (0.0015474 \ mol) \cdot (96485.3 \ C/mol) = 149.31 \ C$

5. Calculate the expected change in mass of copper for each trial. Copper gains two electrons ($Cu^{2+} + 2e^- \rightarrow Cu$). The number of moles of copper deposited will be equal to the number of moles of zinc that dissolved, which we already calculated. $moles_{Cu, trial1} = moles_{Zn, trial1} = 0.0004216 \ mol$ $moles_{Cu, trial2} = moles_{Zn, trial2} = 0.0007737 \ mol$

6. Calculate the mass of Copper deposited for each trial We know that the molar mass of copper is 63.55 g/mol. $Mass = Moles \cdot Molar \ Mass$ For Trial 1: $Mass_{Cu, trial1} = 0.0004216 \ mol \cdot 63.55 \ g/mol = 0.0268 \ g$ For Trial 2: $Mass_{Cu, trial2} = 0.0007737 \ mol \cdot 63.55 \ g/mol = 0.0492 \ g$

7. Calculate the cell efficiency for Trial 1 based on Copper $Efficiency = \frac{Experimental \ change \ in \ mass}{Calculated \ change \ in \ mass} \cdot 100$ Efficiency for Trial 1 based on Copper: $\frac{0.027562 \ g}{0.0268 \ g} \cdot 100 = 102.84 %$

8. Calculate the cell efficiency for Trial 1 based on Zinc Efficiency for Trial 1 based on Zinc: $\frac{0.027562 \ g}{0.027562 \ g} \cdot 100 = 100 %$

9. Calculate the cell efficiency for Trial 2 based on Copper Efficiency for Trial 2 based on Copper: $\frac{0.050584 \ g}{0.0492 \ g} \cdot 100 = 102.81 %$

10. Calculate the cell efficiency for Trial 2 based on Zinc Efficiency for Trial 2 based on Zinc: $\frac{0.050584 \ g}{0.050584 \ g} \cdot 100 = 100 %$