Berechnen Sie dual: 14+11, 14-11; 11-14, 14*11, 14*8
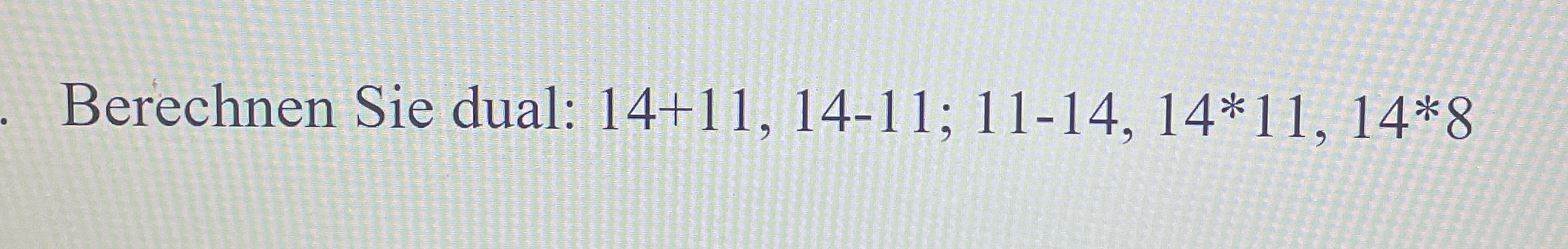
Understand the Problem
Die Frage fordert uns auf, die dualen Darstellungen für die angegebenen mathematischen Operationen zu berechnen. Dies umfasst Addition, Subtraktion und Multiplikation von Zahlen im dualen System.
Answer
- $14 + 11 = 10101$ - $14 - 11 = 0011$ - $11 - 14 = -001$ - $14 * 11 = 10000110$ - $14 * 8 = 1110000$
Answer for screen readers
- $14 + 11 = 10101$
- $14 - 11 = 0011$
- $11 - 14 = -001$
- $14 * 11 = 10000110$
- $14 * 8 = 1110000$
Steps to Solve
- Zahlen in Dual umwandeln
Zuerst wandeln wir die Dezimalzahlen 14 und 11 ins Dualsystem um:
- 14 in Dezimal ist $1110$ in dual.
- 11 in Dezimal ist $1011$ in dual.
- Addition
Um die Summen zu berechnen, addieren wir die beiden dualen Zahlen:
$$ 1110 + 1011 = 1\ 1\ 0\ 1\ 1\ (1) $$
Das Ergebnis ist $1\ 1\ 0\ 0\ 1\ ($ also $10101$ in dual).
- Subtraktion (14 - 11)
Hier subtrahieren wir die dualen Zahlen:
$$ 1110 - 1011 = 0011 $$
Das Ergebnis ist $0011$, was $3$ in Dezimal ist.
- Subtraktion (11 - 14)
Für diese Subtraktion erhalten wir:
$$ 1011 - 1110 $$
Dies führt zu einer negativen Zahl, die wir als $-001$ darstellen können.
- Multiplikation (14 * 11)
Nun multiplizieren wir die beiden dualen Zahlen:
$$ 1110 \times 1011 $$
Wir rechnen wie folgt:
$$ 1110 \times 1011 = 10000110 $$
Das Ergebnis ist $10000110$, was $154$ in Dezimal ist.
- Multiplikation (14 * 8)
Schließlich multiplizieren wir 14 mit 8. Im Dual wird 8 als $1000$ dargestellt:
$$ 1110 \times 1000 $$
Das Ergebnis ist $1110000$, was $112$ in Dezimal ist.
- $14 + 11 = 10101$
- $14 - 11 = 0011$
- $11 - 14 = -001$
- $14 * 11 = 10000110$
- $14 * 8 = 1110000$
More Information
Die duale Darstellung ist wichtig in der Informatik, besonders in der Computerarithmetik. Hierbei werden Zahlen als Binärzahlen (0 und 1) dargestellt, was die Verarbeitung durch Computer erleichtert.
Tips
- Oft wird die Umwandlung von Dezimal zu Dual nicht korrekt durchgeführt. Wichtig ist, die Divisionsmethode oder das wiederholte Subtrahieren von Potenzen von 2 zu verwenden.
- Bei der Addition könnte man Überträge übersehen, was zu falschen Ergebnissen führt.
- Bei der Subtraktion von größeren Zahlen muss man vorsichtig mit der Darstellung negativer Zahlen sein.
AI-generated content may contain errors. Please verify critical information