b = ∑ (5 × 10^i) for i from 0 to n-1
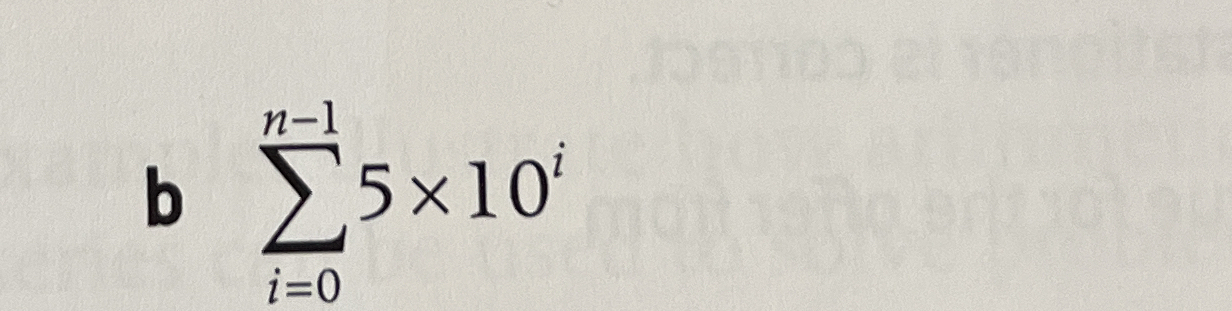
Understand the Problem
The question presents a summation notation that requires evaluating the expression for values of 'i' ranging from 0 to n-1. The goal is to calculate the value of 'b' based on this summation.
Answer
The final answer is $$ b = \frac{5(10^n - 1)}{9} $$
Answer for screen readers
The result is: $$ b = \frac{5(10^n - 1)}{9} $$
Steps to Solve
-
Identify the Summation Expression
The expression is given as ( b = \sum_{i=0}^{n-1} 5 \times 10^i ). This means we will sum the values of ( 5 \times 10^i ) for each integer ( i ) from 0 to ( n-1 ). -
Factor Out the Constant
Since ( 5 ) is constant, we can factor it out of the summation: $$ b = 5 \sum_{i=0}^{n-1} 10^i $$ -
Evaluate the Geometric Series
The summation ( \sum_{i=0}^{n-1} 10^i ) is a geometric series where the first term ( a = 1 ) and the common ratio ( r = 10 ). The formula for the sum of the first ( n ) terms of a geometric series is: $$ S_n = a \frac{r^n - 1}{r - 1} $$ Applying it here gives us: $$ \sum_{i=0}^{n-1} 10^i = \frac{10^n - 1}{10 - 1} = \frac{10^n - 1}{9} $$ -
Substitute Back into the Expression for ( b )
Now we substitute the sum back into the expression for ( b ): $$ b = 5 \cdot \frac{10^n - 1}{9} $$ -
Final Expression for ( b )
Thus, the final expression for ( b ) is: $$ b = \frac{5(10^n - 1)}{9} $$
The result is: $$ b = \frac{5(10^n - 1)}{9} $$
More Information
This formula provides the total for ( b ) based on how many terms ( n ) you're summing. The accumulation follows the principle of geometric series and effectively calculates the total as ( n ) increases.
Tips
- Not recognizing it as a geometric series and incorrectly summing individual terms.
- Forgetting to factor out constants properly, which can lead to complicated calculations.
- Misapplying the parameters in the geometric series formula.
AI-generated content may contain errors. Please verify critical information