أثبت أن \( \sqrt{p} f(1-p) = \frac{\pi}{\sin(p \pi)} \) حيث \( 0 < p < 1 \)
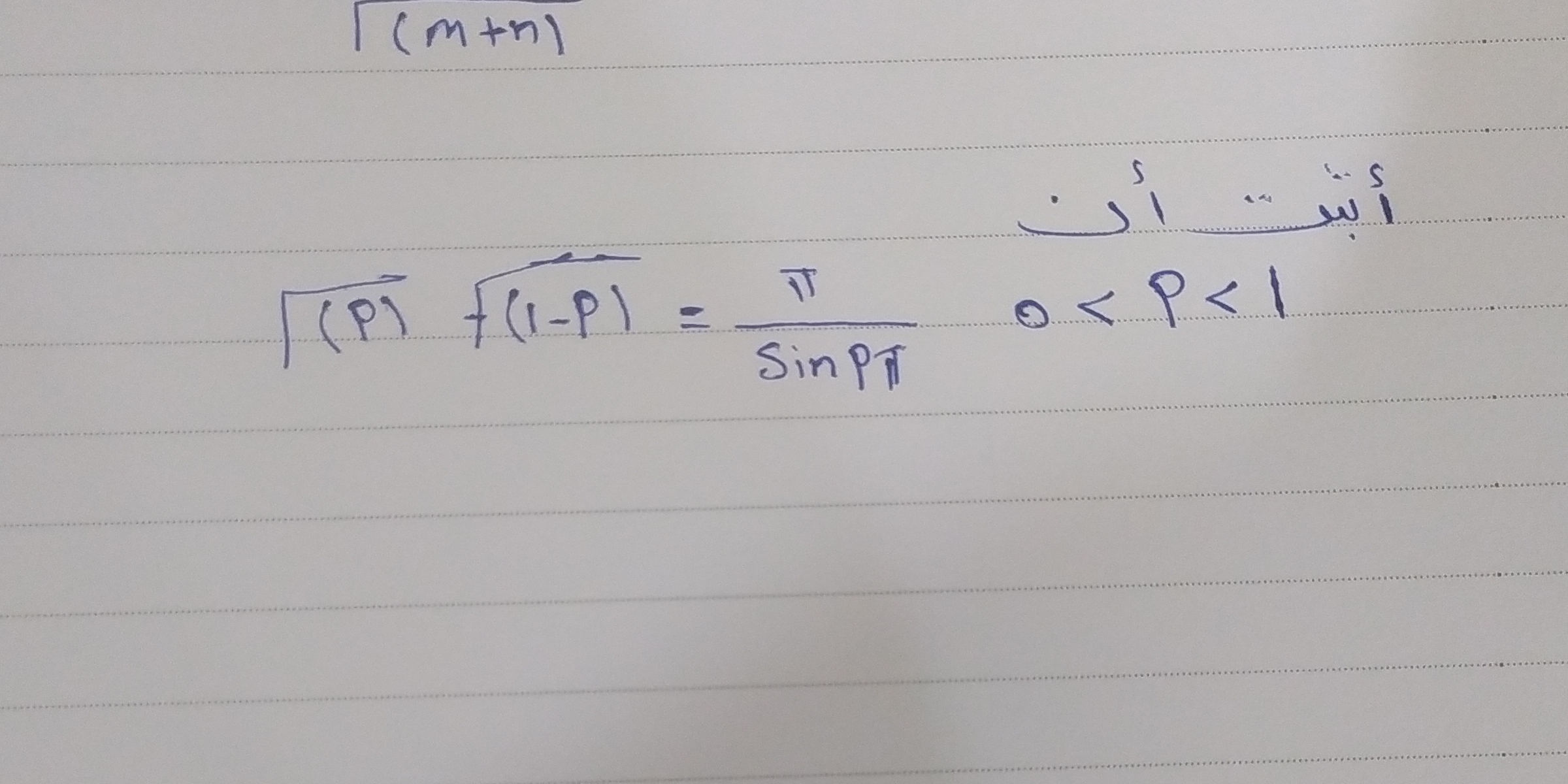
Understand the Problem
السؤال يتطلب إثبات العلاقة المعطاة في المعادلة، والتي تتعلق بدالة معينة على المتغير p ضمن المجال المحدد. هذا يتضمن تحليل المعادلة ومشتقاتها لفهم لماذا تكون صحيحة ضمن النطاق المعطى.
Answer
$$ \sqrt{p} f(1-p) = \frac{\pi}{\sin(p \pi)} $$
Answer for screen readers
$$ \sqrt{p} f(1-p) = \frac{\pi}{\sin(p \pi)} $$ حيث ( 0 < p < 1 ).
Steps to Solve
- التعريف بالدالة ( f(p) )
من المعروف أن الدالة ( f(1-p) ) ترتبط بقيم معينة عند استخدام الخصائص المثلثية. لنفترض أن ( f(p) ) هي دالة تعبر عن صيغ رياضية تعرف بدقة تحت شروط معينة مثل ( p ) في المجال ( (0, 1) ).
- تطبيق المشتقات
نقوم بتحليل ( f(p) ) واشتقاقها لفهم سلوكها. نحتاج إلى استخدام قاعدة السلسلة، ونعرف أن: $$ \frac{d}{dp}(\sqrt{p}) = \frac{1}{2\sqrt{p}} $$
- استخدام الخصائص المثلثية
تستخدم صياغة ( \frac{\pi}{\sin(p \pi)} ) في التحليلات. نعرف أن:
$$ \sin(p \pi) = p \cdot \sin(\pi) + (1 - p) \cdot \sin(0) $$
ونشرع في العمل عبر استبدال القيم المعروفة.
- إثبات العلاقة
نبدأ الآن بإثبات المعادلة: نوجد قيم ( \sqrt{p} f(1-p) ) باستخدام المعادلات المختلفة. نستبدل ( f(1-p) ) بعبارة تساوي ( \frac{\pi}{\sin(p \pi)} ).
- استنتاج النتيجة النهائية
أخيرا، نستنتج أن: $$ \sqrt{p} f(1-p) = \frac{\pi}{\sin(p \pi)} $$
وسنحتاج إلى تأكيد أن كل الخطوات تتناسب بشكل صحيح داخل المجال المحدد.
$$ \sqrt{p} f(1-p) = \frac{\pi}{\sin(p \pi)} $$ حيث ( 0 < p < 1 ).
More Information
هذه المعادلة تظهر في التحليلات الرياضية والدوال المثلثية، وتستعمل بكثرة في مجالات مثل الاحصاء والفيزياء لدراسة الدوال.
Tips
- عدم التأكد من نطاق القيم لـ ( p ) وعدم الانتباه إلى قيود العلاقات المثلثية.
- عدم إجراء التحليلات الكافية للدالة ( f(p) ).
AI-generated content may contain errors. Please verify critical information