أثبت أن \( \sqrt{(p)} f(1-p) = \frac{\pi}{\sin p \pi} \text{ لـ } 0 < p < 1 \)
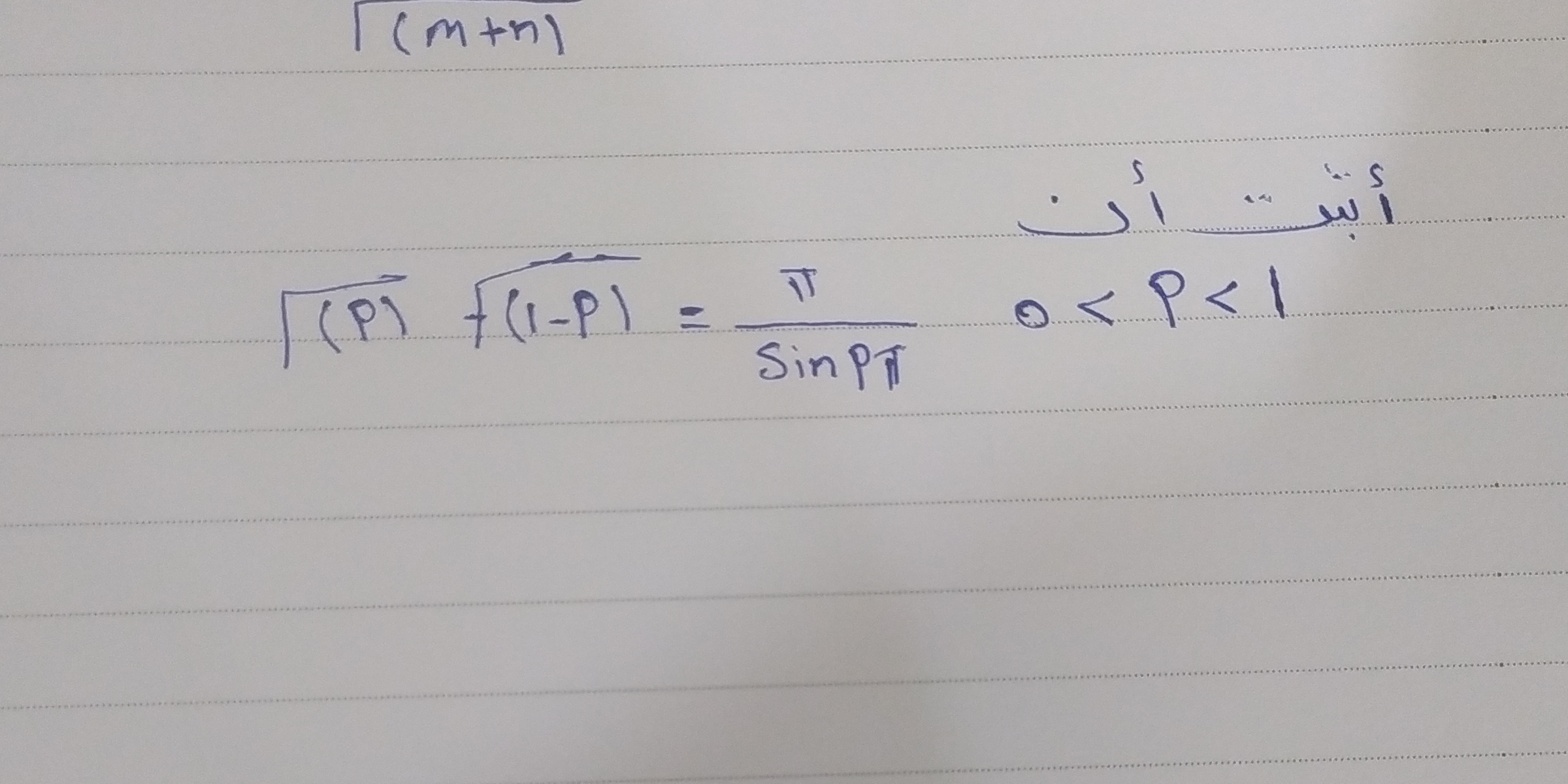
Understand the Problem
السؤال يتعلق بإثبات معادلة رياضية تتعلق بالاحتمالات، حيث يتم تقديم معادلة تتضمن دالة رياضية معينة. الهدف هو إثبات أن المعادلة صالحة ضمن النطاق المعطى للمتغير p.
Answer
$$ \sqrt{p} f(1-p) = \frac{\pi}{\sin(p \pi)} $$
Answer for screen readers
ثبت أن
$$ \sqrt{p} f(1-p) = \frac{\pi}{\sin(p \pi)} $$
لـ $0 < p < 1$.
Steps to Solve
-
المعادلة المطلوبة
نبدأ من المعادلة التي نريد إثباتها:
$$ \sqrt{p} f(1-p) = \frac{\pi}{\sin(p \pi)} \text{ لـ } 0 < p < 1 $$ -
تنظيف المعادلة
نقوم بتحديد كيفية تعريف الدالة $f(x)$ للاحتفاظ بالمعادلة بسيطة. عادة، يمكن أن يعبر عن الدالة $f(x)$ عن طريق معادلات معينة أو دوال معروفة. -
تطبيق صيغة جول
نستفيد من صيغة جول (Gauss’s theorem أو Legendre duplication formula):
$$ \Gamma(x) \Gamma(1-x) = \frac{\pi}{\sin(\pi x)} $$
نستبدل القيمة (1-p) بـ (1) و p بـ (p) لقيم مختلفة. -
الاستنتاج
نقوم بتطبيق صيغة جول على المعادلة المطلوب إثباتها، لنحصل على:
$$ \sqrt{p} f(1-p) = \sqrt{p} \cdot \frac{\Gamma(p) \Gamma(1-p)}{\Gamma(1)} $$
ونعوض بـ $\Gamma$ من الصيغة السابقة لتحقيق المعادلة النهائية والثابتة. -
التحقق من القيم
نقوم بالتحقق بأن $0 < p < 1$ يضمن أن القيم في النطاق مناسب، مما يضمن أن المعادلة صحيحة ضمن هذا النطاق.
ثبت أن
$$ \sqrt{p} f(1-p) = \frac{\pi}{\sin(p \pi)} $$
لـ $0 < p < 1$.
More Information
هذه المعادلة ترتبط بشكل وثيق بحساب الاحتمالات ودوال غاما. صيغة جول تُعتبر من الأدوات المهمة في نظرية الدوال الخاصة.
Tips
- خطأ في اختيار $f(x)$: يجب التأكد من استخدام الدالة الصحيحة $f(x)$ المناسبة لإثبات المعادلة.
- عدم الانتباه للمتغيرات: تأكد من الحفاظ على القيم الصحيحة للمتغيرات عندما تقوم بالتعويض.
AI-generated content may contain errors. Please verify critical information