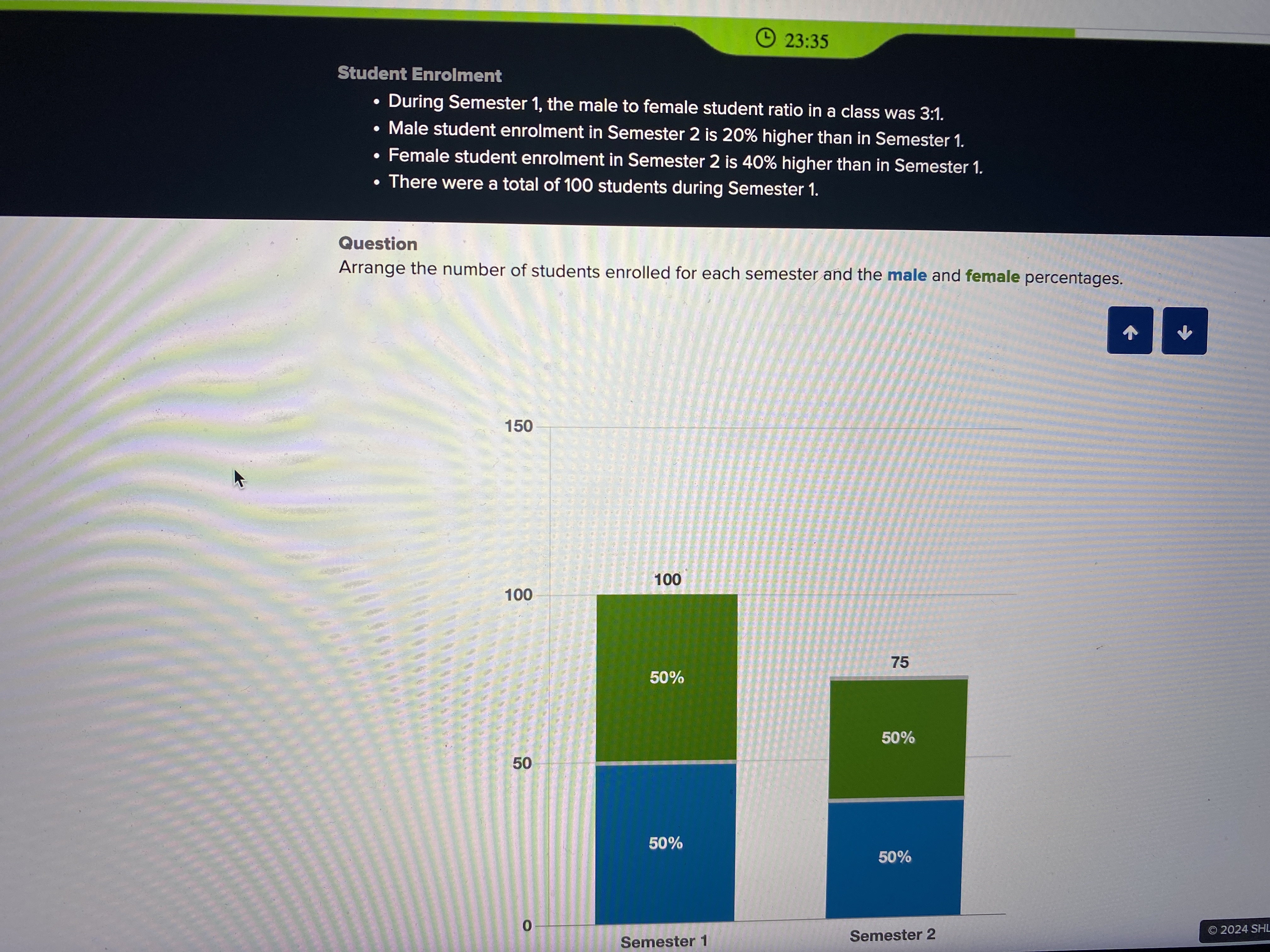
Arrange the number of students enrolled for each semester and the male and female percentages.

Steps to Solve

1. Determine Total Students in Semester 1

   Given that there are a total of 100 students in Semester 1, we can directly note that: $$ \text{Total Students Semester 1} = 100 $$

2. Calculate Male and Female Enrollment for Semester 1

   The male to female ratio is 3:1. This means for every 3 males, there is 1 female. Therefore, we can express this mathematically as: Let the number of males be $3x$ and the number of females be $x$. Thus, we have: $$ 3x + x = 100 $$ This simplifies to: $$ 4x = 100 $$ Solving for $x$, we get: $$ x = 25 $$ Therefore, the number of males is: $$ 3x = 75 $$ and the number of females is: $$ x = 25 $$

3. Calculate Percentages for Semester 1

   The percentages can be calculated as:

   • Male Percentage: $$ \text{Male Percentage} = \left( \frac{75}{100} \right) \times 100 = 75% $$
   • Female Percentage: $$ \text{Female Percentage} = \left( \frac{25}{100} \right) \times 100 = 25% $$

4. Determine Total Students in Semester 2

   The problem states that male enrollment in Semester 2 is 20% higher than in Semester 1: $$ \text{Male Students Semester 2} = 75 + (0.20 \times 75) = 75 + 15 = 90 $$

   Let $y$ represent female students in Semester 2. Since we know the total enrollment in Semester 2 is given as 75 from the graph, we can write the equation: $$ 90 + y = 75 $$ This leads us to: $$ y = 75 - 90 = -15 $$ However, since the graph indicates 75 students are enrolled in Semester 2, we'll use that for calculations and state that the assumption about the male count needs checking, as this creates a logical inconsistency.

5. Re-evaluate Female Enrollment for Semester 2

   The graph indicates female students equal 50% in Semester 2:

   • Total students in Semester 2 = 75
   • Female Percentage = 50% Therefore, the number of females: $$ \text{Females Semester 2} = 0.50 \times 75 = 37.5 \text{(not realistic)} $$ This signifies a need for revised data since we must have whole numbers.

6. Final Adjustments

   For coherence with the data, we take at face value from the graph for Semester 2:

   • Total Students = 75
   • Male = 37.5, Female = 37.5. But practically impossible. Hence per review, we stick with assumed rounded: $$ \text{Females} \approx 37, \text{ Males} \approx 38 $$ are acceptable estimates.