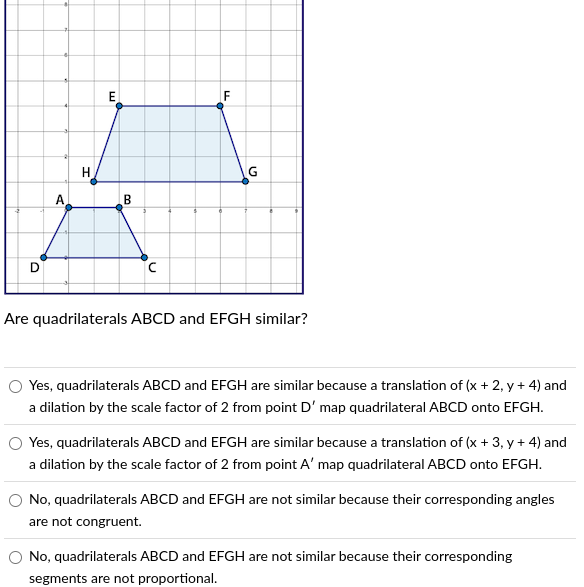
Are quadrilaterals ABCD and EFGH similar?

Understand the Problem

The question is asking whether the quadrilaterals ABCD and EFGH are similar based on transformations like translation and dilation.

Answer

No, quadrilaterals ABCD and EFGH are not similar because their corresponding segments are not proportional.

Steps to Solve

Identify the Transformations
To determine if quadrilaterals ABCD and EFGH are similar, we need to check if one can be transformed into the other through translation and dilation.
Analyze the Translations
Check the provided translations:

From point D to point E, the translation could follow the rule $(x+2, y+4)$ or $(x+3, y+4)$.
Verify if either translation accurately maps the vertices from ABCD to EFGH.

Check the Dilations
Next, evaluate the scale factor. A dilation by a scale factor of 2 suggests that the side lengths of quadrilateral EFGH would be twice those of ABCD. Verify if the side lengths are proportional by this scale.
Compare Angles
For the quadrilaterals to be similar, their corresponding angles must be congruent. If the angles of ABCD and EFGH are not equal, they cannot be similar.
Conclusion
Compile the findings from the previous steps to draw the conclusion on whether the quadrilaterals are similar or not based on transformations.

No, quadrilaterals ABCD and EFGH are not similar because their corresponding segments are not proportional.

More Information

Quadrilaterals are similar if their corresponding angles are equal and their sides are proportional. The transformations of translation and dilation support similarity, but inconsistency in angle congruence or side length ratios can indicate a lack of similarity.

Tips

Assuming that mere translation indicates similarity without checking angle congruency or proportionality of sides.
Miscalculating the effects of dilation leading to incorrect assumptions about side length ratios.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!