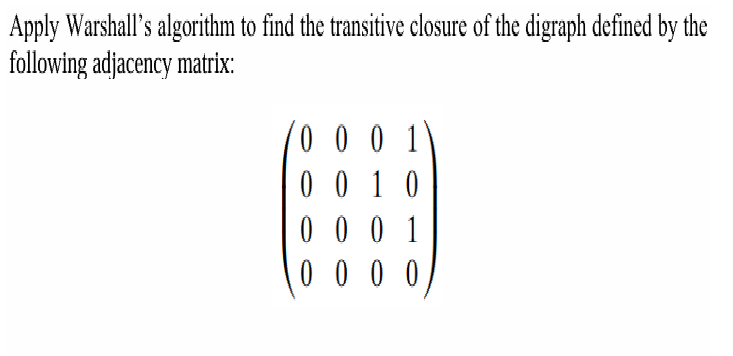
Apply Warshall’s algorithm to find the transitive closure of the digraph defined by the following adjacency matrix: (0 0 0 1; 0 0 1 0; 0 0 1 0; 0 0 0 0)
Understand the Problem
The question is asking to apply Warshall's algorithm to determine the transitive closure of a directed graph represented by a given adjacency matrix. This involves systematically updating the matrix to reflect reachable nodes.
Answer
The transitive closure of the digraph is: $$ \begin{pmatrix} 0 & 0 & 1 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix} $$
Answer for screen readers
The transitive closure of the directed graph is represented by the matrix: $$ \begin{pmatrix} 0 & 0 & 1 & 1 \ 0 & 0 & 1 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 0 \end{pmatrix} $$
Steps to Solve
- Initialize the Adjacency Matrix
Start with the given adjacency matrix representing the directed graph: $$ A = \begin{pmatrix} 0 & 0 & 0 & 1 \ 0 & 0 & 1 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 0 \end{pmatrix} $$
- Apply Warshall’s Algorithm
The algorithm iteratively checks if there's a path between every pair of vertices:
- For each intermediate vertex ( k ), update the matrix: $$ A[i][j] = A[i][j] \lor (A[i][k] \land A[k][j]) $$ Where ( i ) and ( j ) are the vertices being checked.
- Iteration with k = 0
Check if paths exist through vertex 0:
- Update ( A[i][j] ) based on ( A[i][0] ) and ( A[0][j] ): $$ A = \begin{pmatrix} 0 & 0 & 0 & 1 \ 0 & 0 & 1 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 0 \end{pmatrix} $$
No changes occur as ( A[0][:] ) has no outgoing edges.
- Iteration with k = 1
Next, check paths through vertex 1:
- Update ( A[i][j] ) based on ( A[i][1] ) and ( A[1][j] ): $$ A = \begin{pmatrix} 0 & 0 & 1 & 1 \ 0 & 0 & 1 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 0 \end{pmatrix} $$
Now ( A[0][2] ) becomes 1 since there is a path ( 0 \rightarrow 1 \rightarrow 2 ).
- Iteration with k = 2
Now check paths through vertex 2:
- Update ( A[i][j] ): $$ A = \begin{pmatrix} 0 & 0 & 1 & 1 \ 0 & 0 & 1 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 0 \end{pmatrix} $$
No further changes occur.
- Iteration with k = 3
Finally, check paths through vertex 3:
- Update ( A[i][j] ): No changes occur since ( A[3][:] ) has no outgoing edges.
- Final Transitive Closure Matrix
The resulting transitive closure of the graph is: $$ TC = \begin{pmatrix} 0 & 0 & 1 & 1 \ 0 & 0 & 1 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 0 \end{pmatrix} $$
The transitive closure of the directed graph is represented by the matrix: $$ \begin{pmatrix} 0 & 0 & 1 & 1 \ 0 & 0 & 1 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 0 \end{pmatrix} $$
More Information
The transitive closure matrix indicates which vertices are reachable from each vertex in the directed graph. A value of 1 at position ( (i, j) ) means there is a path from vertex ( i ) to vertex ( j ).
Tips
- Not updating every entry: Ensure that every potential path is considered for each intermediate vertex.
- Misinterpreting matrix indices: Remember that matrix indexing starts at 0, which can lead to calculation errors.
- Forgetting logical operations: Use logical AND ($\land$) and logical OR ($\lor$) correctly to update the matrix.
AI-generated content may contain errors. Please verify critical information