أوجد قيمة cscθ إذا كانت tanθ > 0 و secθ = -6/5
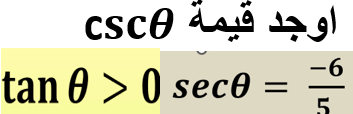
Understand the Problem
السؤال يطلب منا حساب قيمة cscθ مع وجود معطيات حول secθ و tanθ. يتطلب هذا استخدام أساسيات مثل الدوال مثلثية الزاوية وفهم القياسات الرباعية لمثلثات الزاوية.
Answer
\( csc \theta = \frac{6}{\sqrt{11}} \)
Answer for screen readers
[ csc \theta = \frac{6}{\sqrt{11}} \quad \text{أو} \quad csc \theta = \frac{6\sqrt{11}}{11} ]
Steps to Solve
- فهم المعطيات لدينا المعطيات التالية:
- ( \sec \theta = -\frac{6}{5} )
- ( \tan \theta > 0 )
-
استخدام العلاقة بين الدوال المثلثية نستخدم العلاقة ( \sec \theta = \frac{1}{\cos \theta} ) لإيجاد ( \cos \theta ): [ \cos \theta = \frac{1}{\sec \theta} = -\frac{5}{6} ]
-
تحديد نطاق الزاوية بما أن ( \tan \theta > 0 ) و ( \sec \theta < 0 )، فإن الزاوية ( \theta ) تكون في الربع الثاني، حيث تكون الجيب ( \sin \theta ) موجبًا و ( \cos \theta ) سالبًا.
-
استخدام نظرية فيثاغورس نستخدم نظرية فيثاغورس لتحديد قيمة ( \sin \theta ): [ \sin^2 \theta + \cos^2 \theta = 1 ] [ \sin^2 \theta + \left(-\frac{5}{6}\right)^2 = 1 ] [ \sin^2 \theta + \frac{25}{36} = 1 ] [ \sin^2 \theta = 1 - \frac{25}{36} = \frac{11}{36} ]
-
حساب قيمة ( \sin \theta ) نأخذ الجذر التربيعي: [ \sin \theta = \sqrt{\frac{11}{36}} = \frac{\sqrt{11}}{6} ] وبما أن ( \sin \theta ) موجب في الربع الثاني: [ \sin \theta = \frac{\sqrt{11}}{6} ]
-
حساب ( csc \theta ) الآن نحسب قيمة ( csc \theta ): [ csc \theta = \frac{1}{\sin \theta} = \frac{6}{\sqrt{11}} ]
-
تأمين الجواب النهائي يمكن أيضًا تربيع الكسر: [ csc \theta = \frac{6\sqrt{11}}{11} ]
[ csc \theta = \frac{6}{\sqrt{11}} \quad \text{أو} \quad csc \theta = \frac{6\sqrt{11}}{11} ]
More Information
في هذا السؤال، استخدمنا قوانين الدوال المثلثية لحساب قيمة ( csc \theta ) بناءً على المعطيات المعطاة. تعتبر هذه الأمور أساسية في دراسة المثلثات.
Tips
- عدم الانتباه إلى إشارة ( \sec \theta ) مما يؤدي إلى نتائج خاطئة في تحديد الربع الذي توجد فيه الزاوية.
- نسيان أن قيم الجيب و الجيب التمام لها إشارات مختلفة في الأرباع المختلفة.
AI-generated content may contain errors. Please verify critical information