Analyze the given functions: f1(x) = x, f2(x) = x^2, f3(x) = √x, f4(x) = x^3, f5(x) = -x - 2, f6(x) = x + 2.
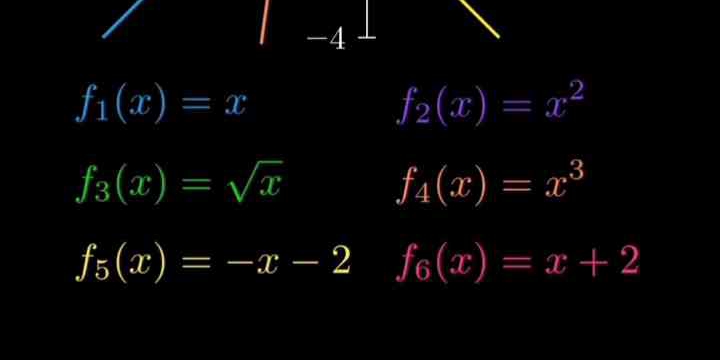
Understand the Problem
The question lists six mathematical functions, and it may be asking for a specific analysis or evaluation of these functions. The high-level approach involves determining characteristics such as their properties or the relationships between them.
Answer
The functions exhibit diverse properties: $f_1, f_4, f_5$ are linear or odd; $f_2$ is even and quadratic; $f_3$ is a square root; and $f_6$ is linear.
Answer for screen readers
Characteristics of the functions have been detailed, including their types, domains, ranges, continuity, behaviors, symmetries, and special points.
Steps to Solve
-
Identify the Functions and Their Forms
The functions provided are:
- $f_1(x) = x$ (linear function)
- $f_2(x) = x^2$ (quadratic function)
- $f_3(x) = \sqrt{x}$ (square root function)
- $f_4(x) = x^3$ (cubic function)
- $f_5(x) = -x - 2$ (linear function)
- $f_6(x) = x + 2$ (linear function)
-
Analyze Each Function's Characteristics
Evaluate the properties including:
-
Domain and Range:
- $f_1(x)$: Domain: all real numbers; Range: all real numbers.
- $f_2(x)$: Domain: all real numbers; Range: $[0, \infty)$.
- $f_3(x)$: Domain: $[0, \infty)$; Range: $[0, \infty)$.
- $f_4(x)$: Domain: all real numbers; Range: all real numbers.
- $f_5(x)$: Domain: all real numbers; Range: all real numbers.
- $f_6(x)$: Domain: all real numbers; Range: all real numbers.
-
Domain and Range:
-
Determine Continuity and Behavior
- Check for continuity over their domains. All listed functions are continuous within their defined domains.
- Analyze end behavior:
- $f_1(x)$: increases without bound.
- $f_2(x)$: increases rapidly as $x$ moves away from zero.
- $f_3(x)$: increases but at a decreasing rate.
- $f_4(x)$: increases dramatically as $x$ grows large.
- $f_5(x)$: decreases without bound.
- $f_6(x)$: increases linearly.
-
Assess Symmetry
- Check for symmetry:
- $f_1(x)$: Odd function (symmetric about origin).
- $f_2(x)$: Even function (symmetric about $y$-axis).
- $f_3(x)$: Neither even nor odd.
- $f_4(x)$: Odd function.
- $f_5(x)$: Odd function.
- $f_6(x)$: Neither even nor odd.
- Check for symmetry:
-
Evaluate Special Points
- Identify key features like intercepts and turning points:
- $f_1(x)$: Intercept at (0,0).
- $f_2(x)$: Intercept at (0,0).
- $f_3(x)$: Intercept at (0,0).
- $f_4(x)$: Intercept at (0,0).
- $f_5(x)$: Intercept at (-2,0).
- $f_6(x)$: Intercept at (-2,0).
- Identify key features like intercepts and turning points:
Characteristics of the functions have been detailed, including their types, domains, ranges, continuity, behaviors, symmetries, and special points.
More Information
These functions represent a variety of mathematical forms that are fundamental in calculus and algebra. Understanding their behaviors is crucial in graphing and analyzing behavior in applied mathematics.
Tips
- Confusing the domain and range of square root functions.
- Overlooking that not all polynomials have the same end behavior.
- Misclassifying functions as even or odd without proper analysis.
AI-generated content may contain errors. Please verify critical information