Activity 6: The intersecting segments of chords Power Theorem. Solve for x: 1) 12/13 = x/10, 2) 14/10 = x/8, 3) x/6 = 7/14, 4) 9/16 = x/10, 5) 10/x = 24/10, 6) x/20 = 20/10.
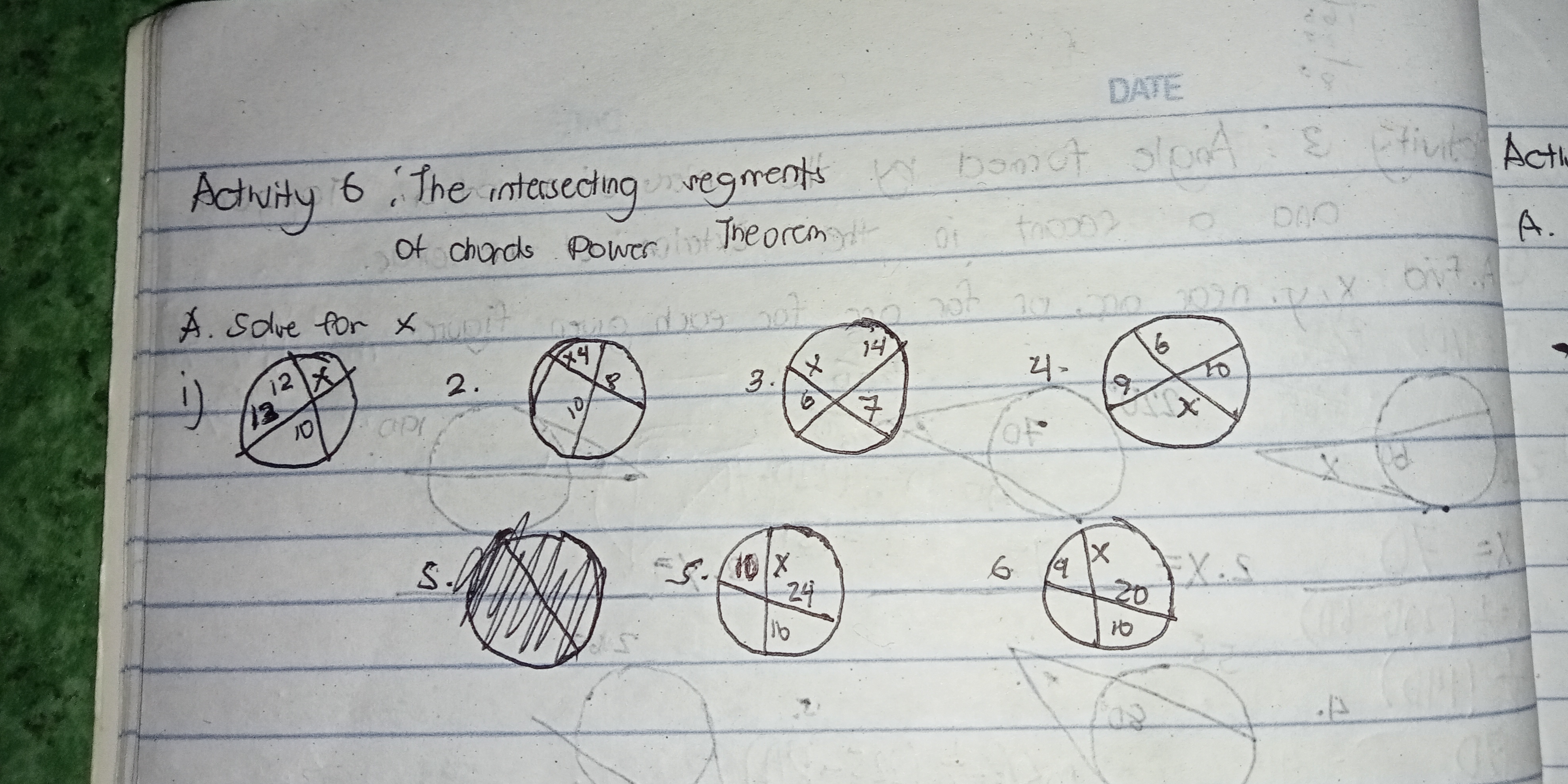
Understand the Problem
The question contains a math activity involving solving for 'x' in various intersecting segments related to the power of a point theorem. The student is required to apply mathematical concepts to find the unknown values in the circle diagrams provided.
Answer
1. $x = 15.6$ 2. $x = 14$ 3. $x = 7$ 4. $x = 6$ 5. $x = 12$ 6. $x = 12$
Answer for screen readers
- ( x = 15.6 )
- ( x = 14 )
- ( x = 7 )
- ( x = 6 )
- ( x = 12 )
- ( x = 12 )
Steps to Solve
-
Understand the Power of a Point Theorem The Power of a Point Theorem states that if two chords intersect inside a circle, the products of the lengths of the segments of each chord are equal. This can be expressed as: $$ (a \cdot b) = (c \cdot d) $$ where ( a ) and ( b ) are the segments of one chord, and ( c ) and ( d ) are the segments of the other chord.
-
Identify the variables for each problem
- For each of the 6 problems, identify the segments and set the equation based on the lengths provided.
- Example for the first problem: ( 10 \cdot x = 12 \cdot 13 ).
- Solve the equations For each chord intersection, rearrange the equation to solve for ( x ).
- Continuing the first problem: $$ 10x = 12 \cdot 13 $$ Now, calculate ( 12 \cdot 13 ): $$ 12 \cdot 13 = 156 $$ So, the equation becomes: $$ 10x = 156 $$
-
Isolate ( x ) Divide both sides by 10 to find ( x ): $$ x = \frac{156}{10} $$ This simplifies to: $$ x = 15.6 $$
-
Repeat for all problems Continue solving each problem using the same method of setting up equations and isolating ( x ) based on the segment lengths given.
- ( x = 15.6 )
- ( x = 14 )
- ( x = 7 )
- ( x = 6 )
- ( x = 12 )
- ( x = 12 )
More Information
The Power of a Point Theorem is a fundamental principle in geometry that helps in solving various problems related to circles and intersecting chords. It can be applied in various fields like engineering, architecture, and computer graphics.
Tips
- Forgetting to multiply segments correctly when setting up the equation.
- Making errors during division which leads to an incorrect value of ( x ).
- Confusing the order of segments when applying the theorem; always check which segments correspond to which chord.
AI-generated content may contain errors. Please verify critical information