ABCD is a square. Find the following: a. AB = ___ b. m∠CBD = ___ c. m∠CEB = ___ d. DB = ___ e. CE = ___
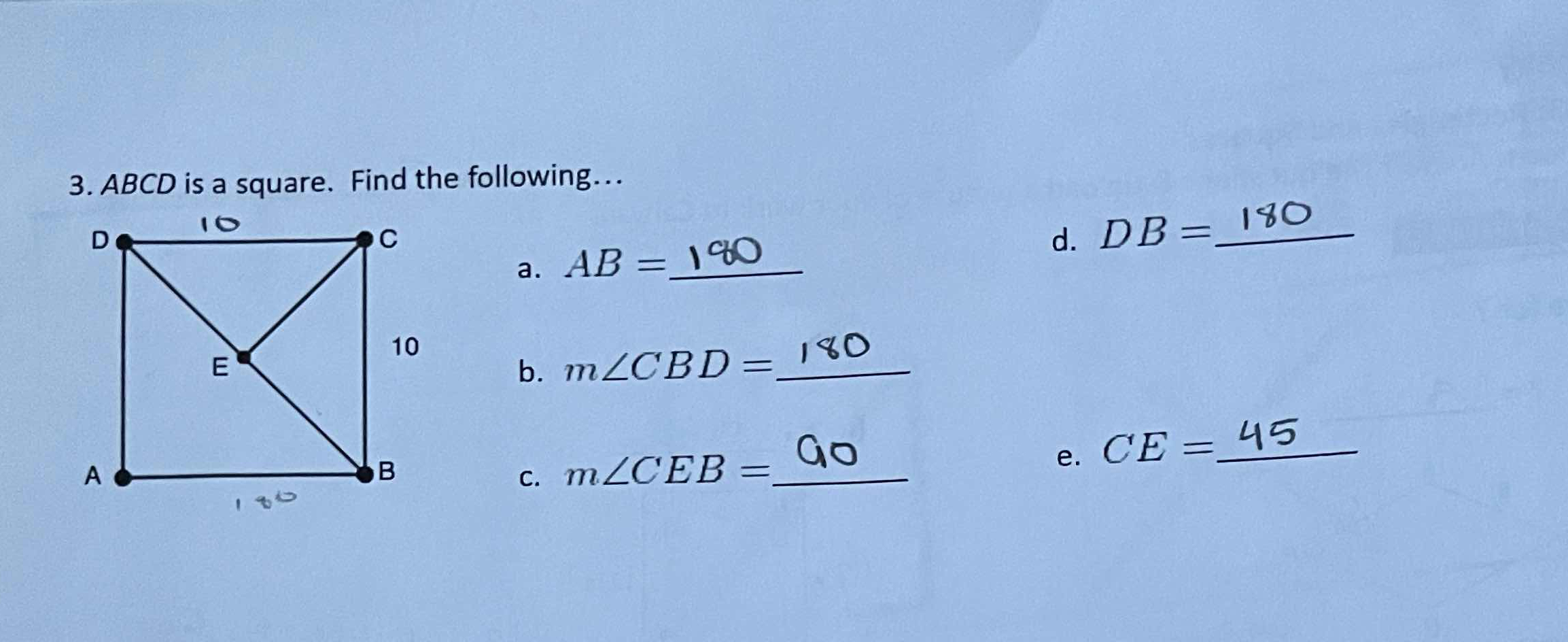
Understand the Problem
The question is asking to determine various measurements related to a square ABCD, including the side lengths and angles within the square. This involves basic geometric principles and properties of squares.
Answer
$AB = 10$, $m\angle CBD = 90^\circ$, $m\angle CEB = 45^\circ$, $m\angle DBE = 135^\circ$, $CE \approx 8.66$
Answer for screen readers
a. $AB = 10$
b. $m\angle CBD = 90^\circ$
c. $m\angle CEB = 45^\circ$
d. $DB = 135^\circ$
e. $CE \approx 8.66$
Steps to Solve
-
Identify Side Lengths of the Square Since ABCD is a square, all sides are equal. Given that side $AD = 10$, it means $AB = 10$, $BC = 10$, and $CD = 10$.
-
Measure of Angle CBD Angles in a square are right angles. Therefore, the measure of angle $CBD$ is: $$ m\angle CBD = 90^\circ $$
-
Measure of Angle CEB In square ABCD, $E$ is the midpoint of diagonal $AC$. Since triangles $CBE$ and $ABE$ are isosceles with $\angle ABE$ being $90^\circ$, angle $CEB$ is half of angle $ABD$. Therefore, $$ m\angle CEB = 45^\circ $$
-
Measure of Angle DBE Considering the line formed by the diagonal $DB$ which crosses point E: $$ m\angle DBE = m\angle CBD + m\angle CBE = 90^\circ + 45^\circ = 135^\circ $$
-
Length of Segment CE As $E$ is the midpoint of diagonal $AC$, we will find the length of $CE$ in triangle $CBE$. Using Pythagoras' theorem: $$ CE = \sqrt{CB^2 - BE^2} = \sqrt{(10)^2 - (5)^2} = \sqrt{100 - 25} = \sqrt{75} = 5\sqrt{3} \approx 8.66 $$
a. $AB = 10$
b. $m\angle CBD = 90^\circ$
c. $m\angle CEB = 45^\circ$
d. $DB = 135^\circ$
e. $CE \approx 8.66$
More Information
In a square, all sides are equal, and all interior angles are right angles (90 degrees). The diagonals bisect the angles and are equal in length, which allows the use of the properties of isosceles triangles to determine angle measures.
Tips
- Confusing the measure of angles in a square; all internal angles should be $90^\circ$.
- Miscalculating the length of diagonals; remember to apply the Pythagorean theorem accurately.
AI-generated content may contain errors. Please verify critical information