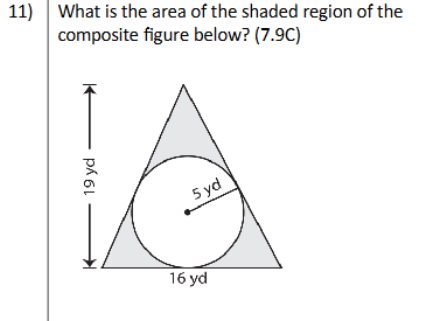
What is the area of the shaded region of the composite figure below? The figure is a triangle with a circle inscribed in it. The height of the triangle is 19 yards, the base is 16... What is the area of the shaded region of the composite figure below? The figure is a triangle with a circle inscribed in it. The height of the triangle is 19 yards, the base is 16 yards, and the radius of the circle is 5 yards.
Understand the Problem
The question asks to calculate the area of the shaded region in the composite figure. This involves finding the area of the triangle, finding the area of the circle, and then subtracting the area of circle from the area of the triangle.
Answer
$73.5$ square yards
Answer for screen readers
$73.5$ square yards
Steps to Solve
- Find the area of the triangle
The area of a triangle is given by the formula: $A_{triangle} = \frac{1}{2} \times base \times height$. The base of the triangle is 16 yd and the height is 19 yd.
$A_{triangle} = \frac{1}{2} \times 16 \times 19 = 8 \times 19 = 152$ square yards.
- Find the area of the circle
The area of a circle is given by the formula: $A_{circle} = \pi \times r^2$, where $r$ is the radius of the circle. The radius of the circle is 5 yd. Use $\pi \approx 3.14$.
$A_{circle} = \pi \times 5^2 = 3.14 \times 25 = 78.5$ square yards.
- Subtract the area of the circle from the area of the triangle to find the area of shaded region
$A_{shaded} = A_{triangle} - A_{circle} = 152 - 78.5 = 73.5$ square yards.
$73.5$ square yards
More Information
The area of the shaded region is found by subtracting the area of the unshaded region (circle) from the total area of the triangle
Tips
A common mistake is using the diameter instead of the radius when calculating the area of the circle. Remember that the radius is half the diameter.
AI-generated content may contain errors. Please verify critical information