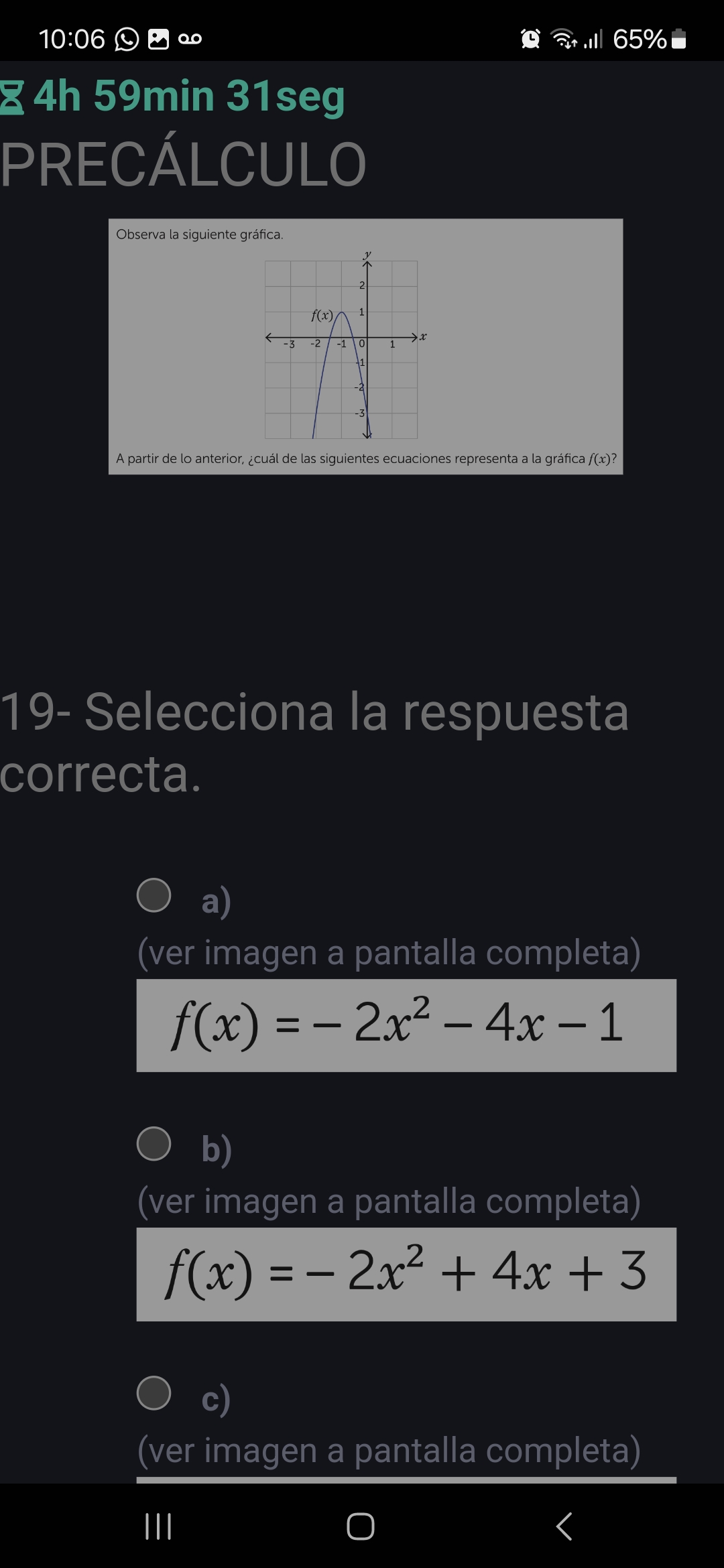
A partir de la gráfica de f(x), ¿cuál de las siguientes ecuaciones representa a la gráfica f(x)? a) f(x) = -2x^2 - 4x - 1 b) f(x) = -2x^2 + 4x + 3 c) (ver imagen a pantalla complet... A partir de la gráfica de f(x), ¿cuál de las siguientes ecuaciones representa a la gráfica f(x)? a) f(x) = -2x^2 - 4x - 1 b) f(x) = -2x^2 + 4x + 3 c) (ver imagen a pantalla completa)
Understand the Problem
La pregunta te pide que identifiques cuál de las ecuaciones cuadráticas dadas corresponde a la gráfica de la función f(x) mostrada. Para resolverlo, debes analizar la gráfica para identificar puntos clave (como el vértice y las intersecciones con los ejes) y luego comparar estos puntos con las ecuaciones proporcionadas.
Answer
a) $f(x) = -2x^2 - 4x - 1$
Answer for screen readers
a) $f(x) = -2x^2 - 4x - 1$
Steps to Solve
- Identify key features of the graph
The graph is a parabola that opens downwards, meaning the coefficient of the $x^2$ term is negative. The vertex appears to be at the point $(-1, 1)$. The y-intercept appears to be approximately at $(0, -1)$.
- Analyze option a: $f(x) = -2x^2 - 4x - 1$
To find the vertex, we can use the formula $x = -\frac{b}{2a}$. In this case, $a = -2$ and $b = -4$, so $x = -\frac{-4}{2(-2)} = -\frac{-4}{-4} = -1$.
Now, find the $y$-coordinate of the vertex by substituting $x = -1$ into the equation:
$f(-1) = -2(-1)^2 - 4(-1) - 1 = -2(1) + 4 - 1 = -2 + 4 - 1 = 1$. Therefore, the vertex is $(-1, 1)$.
The $y$-intercept can be found by setting $x = 0$:
$f(0) = -2(0)^2 - 4(0) - 1 = -1$. Therefore, the $y$-intercept is $(0, -1)$.
- Analyze option b: $f(x) = -2x^2 + 4x + 3$
To find the vertex, we can use the formula $x = -\frac{b}{2a}$. In this case, $a = -2$ and $b = 4$, so $x = -\frac{4}{2(-2)} = -\frac{4}{-4} = 1$.
Now, find the $y$-coordinate of the vertex by substituting $x = 1$ into the equation:
$f(1) = -2(1)^2 + 4(1) + 3 = -2(1) + 4 + 3 = -2 + 4 + 3 = 5$. Therefore, the vertex is $(1, 5)$. This is not the vertex that we had identified initially
- Compare the identified point with the equations Option a has a vertex of $(-1, 1)$ and a y-intercept of $(0, -1)$, which matches the graph. Option b has a vertex of $(1, 5)$ which is already incorrect. Therefore, we can conclude the option a) is the correct answer.
a) $f(x) = -2x^2 - 4x - 1$
More Information
The vertex form of a quadratic equation is $f(x) = a(x-h)^2 + k$, where $(h, k)$ is the vertex of the parabola. This form can be useful for quickly identifying the vertex of a given quadratic function.
Tips
A common mistake is incorrectly calculating the x-coordinate of the vertex using the formula $x = -\frac{b}{2a}$. Ensure you correctly identify $a$ and $b$ and substitute them carefully into the formula. Another common mistake is making an error when evaluating the function at a specific $x$-value.
AI-generated content may contain errors. Please verify critical information