AB^2 = 1+1-2(cos(α)cos(β)+sin(α)sin(β)) AB^2 = 2[1-cos(α-β)]
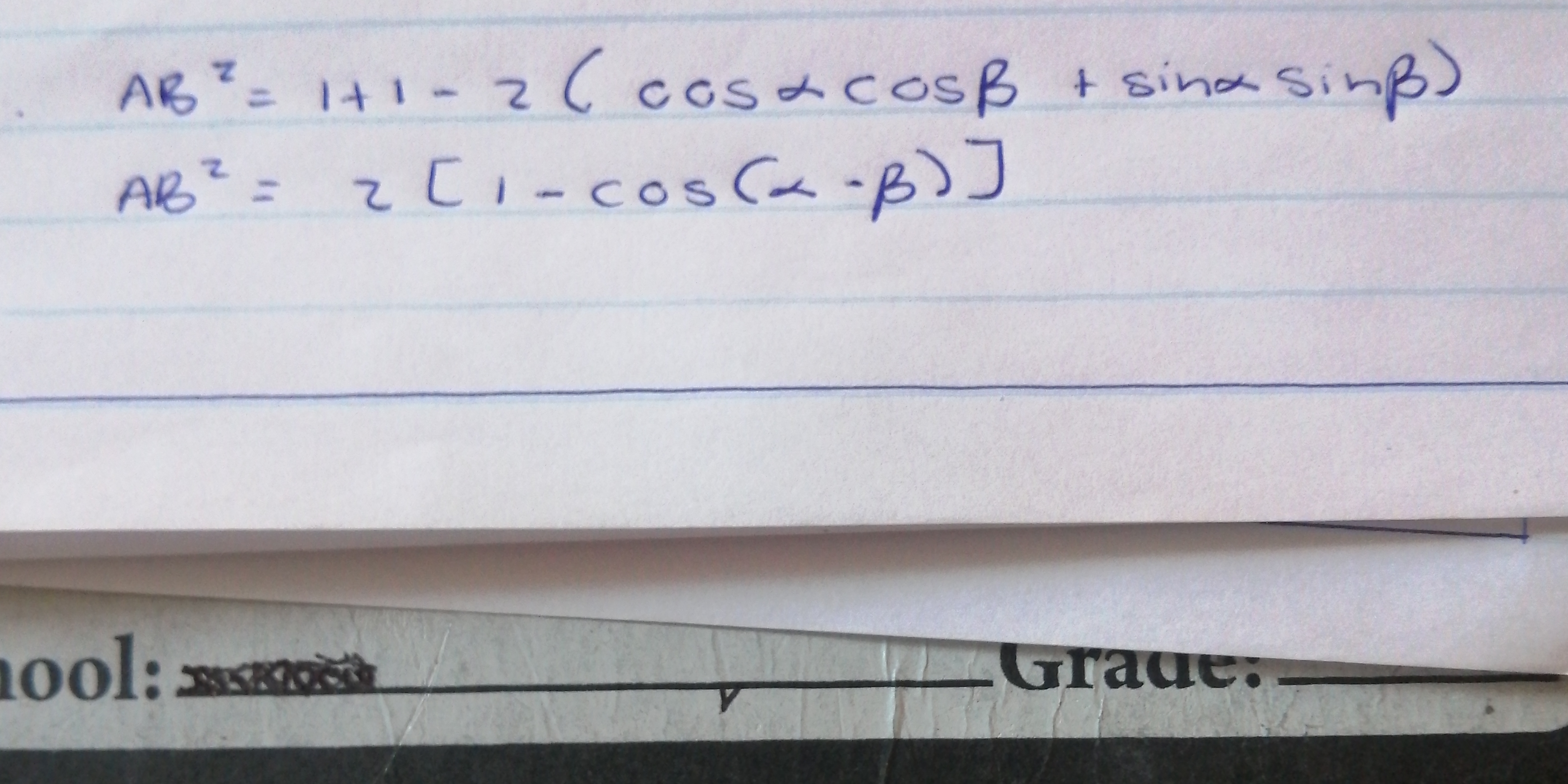
Understand the Problem
The question presents two equations and appears to be related to trigonometric identities, specifically the cosine subtraction formula. The goal is likely either to prove the second equation based on the first, or to simplify some trigonometric expression.
Answer
$AB^2 = 2[1 - \cos(\alpha - \beta)]$
Answer for screen readers
$AB^2 = 2[1 - \cos(\alpha - \beta)]$
Steps to Solve
- Simplify the first equation
Starting from the first equation, combine the constants: $$ AB^2 = 1 + 1 - 2(\cos\alpha \cos\beta + \sin\alpha \sin\beta) $$ $$ AB^2 = 2 - 2(\cos\alpha \cos\beta + \sin\alpha \sin\beta) $$
- Apply the cosine subtraction formula
Use the trigonometric identity for the cosine of a difference: $$ \cos(\alpha - \beta) = \cos\alpha \cos\beta + \sin\alpha \sin\beta $$ Substitute this into the equation: $$ AB^2 = 2 - 2 \cos(\alpha - \beta) $$
- Factor out the constant
Factor out a $2$ from the right side: $$ AB^2 = 2(1 - \cos(\alpha - \beta)) $$
This is the second equation, so the derivation is complete.
$AB^2 = 2[1 - \cos(\alpha - \beta)]$
More Information
The formula shown is often used in geometry and physics, particularly when calculating distances based on angles. One application involves finding the distance between two points on a sphere given their latitudes and longitudes. The derivation relies on fundamental trigonometric identities.
Tips
A common mistake is to incorrectly apply the cosine subtraction or addition formulas. It's crucial to remember the correct formula: $\cos(\alpha - \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta$. Also, be careful with signs when manipulating trigonometric identities; a wrong sign can lead to an incorrect result.
AI-generated content may contain errors. Please verify critical information