a^2 - 2ab + b^2 - c^2 = (p) m^2 + 2mn + n^2 - k^2 = (q) p^2 - 2pq + q^2 - 4 = (r) 4 - a^2 - 2ab - b^2 = (s) k^3 + k^2 - k - 1 = (t) t^4 - t^3 - t - 1 = (u) a^2 + 2ab + b^2 -... a^2 - 2ab + b^2 - c^2 = (p) m^2 + 2mn + n^2 - k^2 = (q) p^2 - 2pq + q^2 - 4 = (r) 4 - a^2 - 2ab - b^2 = (s) k^3 + k^2 - k - 1 = (t) t^4 - t^3 - t - 1 = (u) a^2 + 2ab + b^2 - ac - bc = (v)
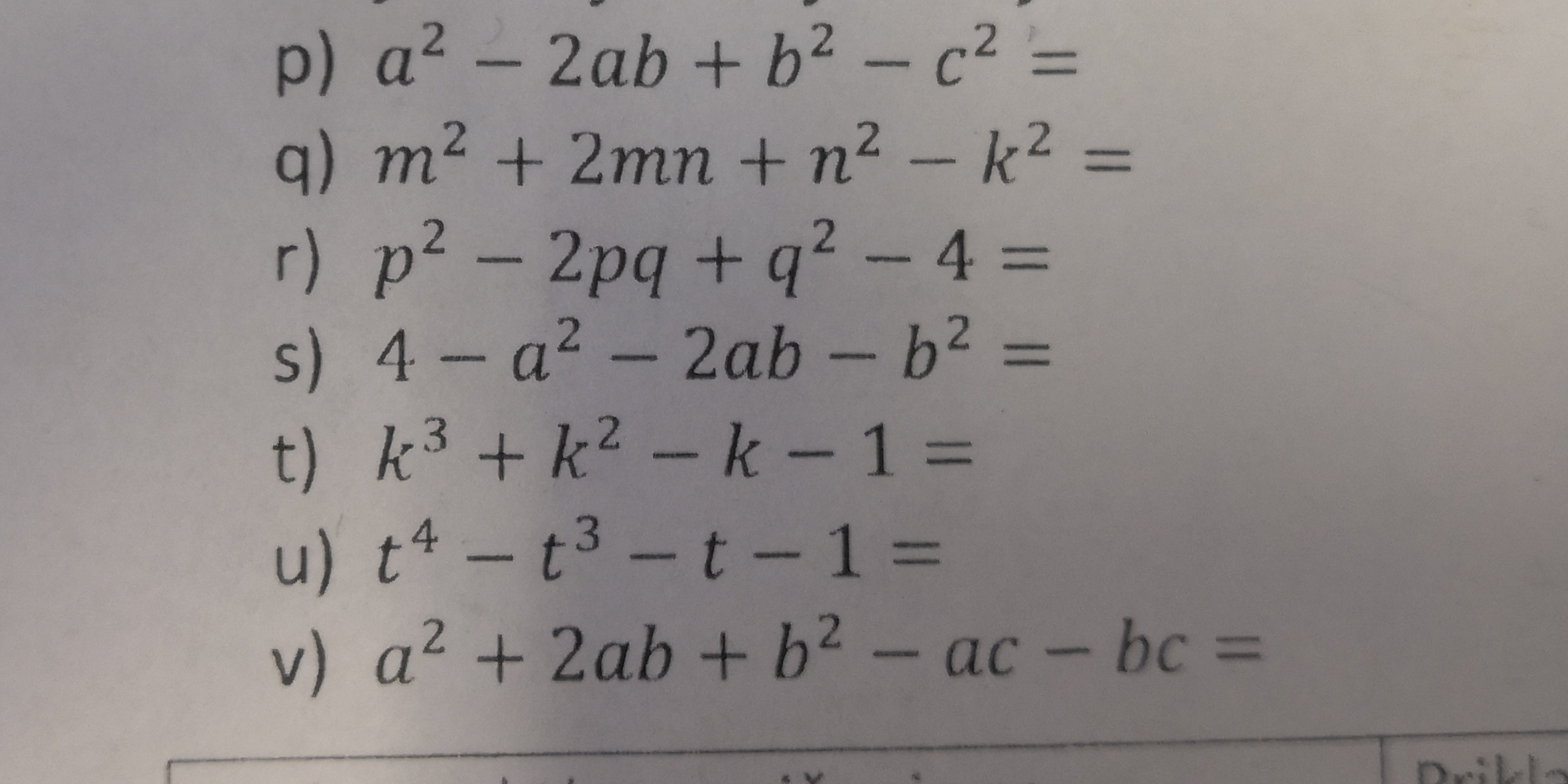
Understand the Problem
The question presents a list of algebraic expressions that seem to be related to mathematical problems involving simplification or factorization. Each expression likely requires a separate analysis or application of algebraic identities to solve.
Answer
- p) $(a-b-c)(a-b+c)$ - q) $(m+n-k)(m+n+k)$ - r) $(p-q-2)(p-q+2)$ - s) $-(a+b-2)(a+b+2)$ - t) $(k-1)(k+1)^2$ - u) Needs further analysis - v) $(a+b-c)(a+b)$
Answer for screen readers
- p) $(a-b-c)(a-b+c)$
- q) $(m+n-k)(m+n+k)$
- r) $(p-q-2)(p-q+2)$
- s) $-(a+b-2)(a+b+2)$
- t) $(k-1)(k+1)^2$
- u) Needs further analysis
- v) $(a+b-c)(a+b)$
Steps to Solve
-
Expression p: Factorization of $a^2 - 2ab + b^2 - c^2$ To factor this expression, we can first identify a perfect square and then apply the difference of squares: $$ a^2 - 2ab + b^2 = (a-b)^2 $$ Thus, the expression simplifies to: $$ (a - b)^2 - c^2 $$ This can be further factored using the difference of squares: $$ (a-b-c)(a-b+c) $$
-
Expression q: Factor $m^2 + 2mn + n^2 - k^2$ This is a sum of squares minus a square: $$ m^2 + 2mn + n^2 = (m + n)^2 $$ So we rewrite it: $$ (m+n)^2 - k^2 $$ This can be factored as: $$ (m+n-k)(m+n+k) $$
-
Expression r: Simplify $p^2 - 2pq + q^2 - 4$ Here, we identify: $$ p^2 - 2pq + q^2 = (p-q)^2 $$ So the expression becomes: $$ (p-q)^2 - 4 $$ Using difference of squares: $$ (p-q-2)(p-q+2) $$
-
Expression s: Simplify $4 - a^2 - 2ab - b^2$ Rearranging gives: $$ - (a^2 + 2ab + b^2 - 4) = -((a+b)^2 - 4) $$ Factoring this using the difference of squares: $$ -(a+b-2)(a+b+2) $$
-
Expression t: Simplify $k^3 + k^2 - k - 1$ Factor out the common terms: $$ k^2(k + 1) - 1 = (k^2 - 1)(k + 1) $$ This can be factored further: $$ (k-1)(k+1)(k+1) = (k-1)(k+1)^2 $$
-
Expression u: Simplify $t^4 - t^3 - t - 1$ Group terms: $$ t^3(t-1) - 1 $$ Using rational root theorem or synthetic division could be helpful.
-
Expression v: Simplify $a^2 + 2ab + b^2 - ac - bc$ Rearranging the terms gives: $$ (a^2 + 2ab + b^2) - (ac + bc) = (a+b)^2 - c(a+b) $$ Therefore: $$ (a + b - c)(a + b) $$
- p) $(a-b-c)(a-b+c)$
- q) $(m+n-k)(m+n+k)$
- r) $(p-q-2)(p-q+2)$
- s) $-(a+b-2)(a+b+2)$
- t) $(k-1)(k+1)^2$
- u) Needs further analysis
- v) $(a+b-c)(a+b)$
More Information
These expressions are primarily a mix of perfect square identifications and applications of the difference of squares. Taking notice of the forms to identify factorizable patterns is key in these problems.
Tips
- Not recognizing perfect square patterns, particularly in expressions like $a^2 - 2ab + b^2$.
- Forgetting to apply the difference of squares when it is possible.
- Failing to reorganize terms can lead to missing simpler forms.
AI-generated content may contain errors. Please verify critical information