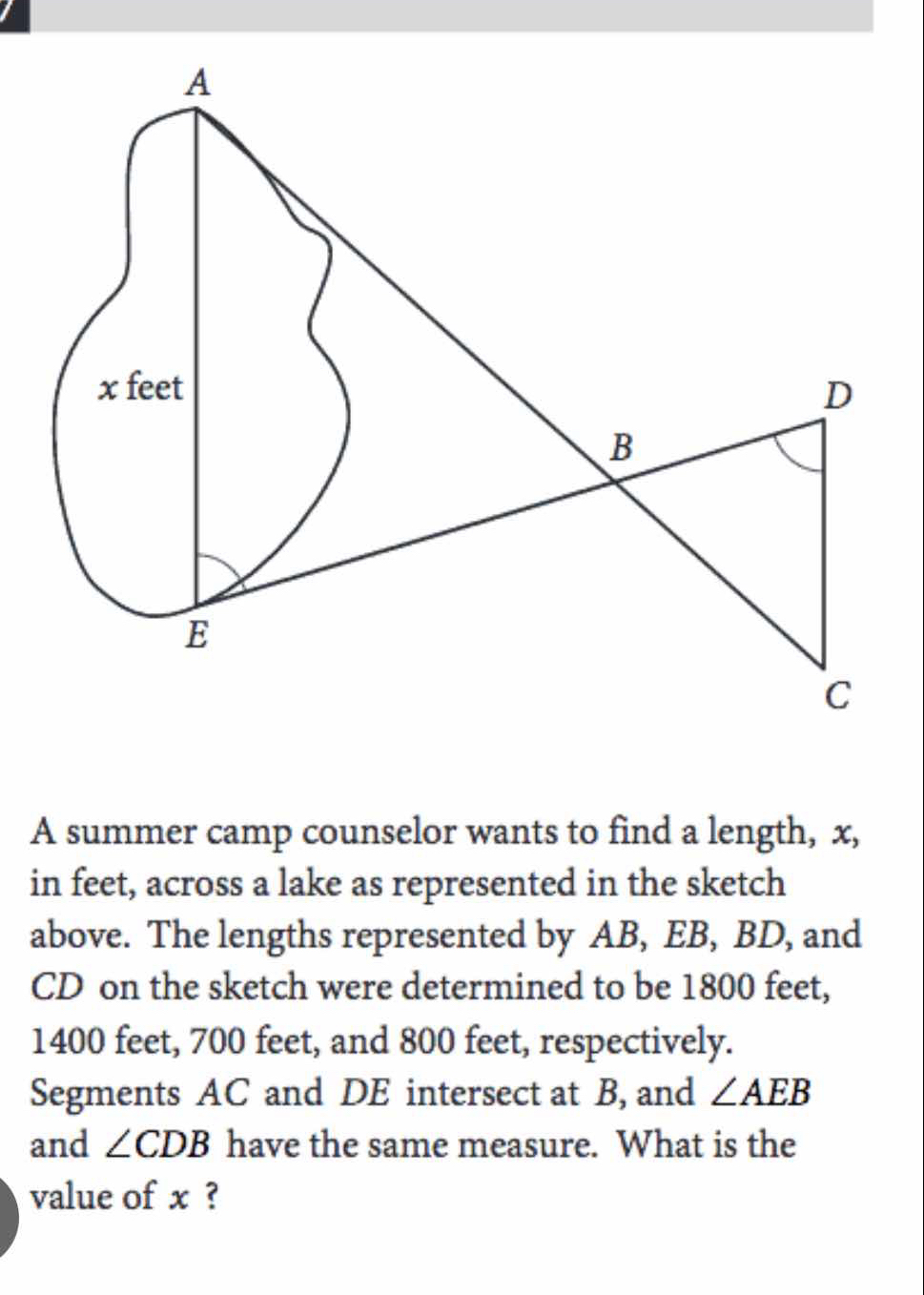
A summer camp counselor wants to find a length, x, in feet across a lake as represented in the sketch above. The lengths represented by AB, EB, BD, and CD on the sketch were determ... A summer camp counselor wants to find a length, x, in feet across a lake as represented in the sketch above. The lengths represented by AB, EB, BD, and CD on the sketch were determined to be 1800 feet, 1400 feet, 700 feet, and 800 feet, respectively. Segments AC and DE intersect at B, and angles AEB and CDB have the same measure. What is the value of x? Read more

Steps to Solve

1. Identify the Triangles Involved

   The segments intersect at point B, forming triangle AEB and triangle CDB, where $AB = 1800$ feet, $EB = 1400$ feet, $BD = 700$ feet, and $CD = 800$ feet.

2. Use Angle Properties

   Since angles $\angle AEB$ and $\angle CDB$ are equal, we can use the property of similar triangles. The segments across both triangles give us the relationship:

   $$ \frac{AB}{EB} = \frac{CD}{BD} $$

3. Plug in the Known Values

   Substitute the values of the segments into the ratio:

   $$ \frac{1800}{1400} = \frac{800}{700} $$

4. Cross-Multiply to Solve for x

   First, simplify the fractions:

   $$ \frac{18}{14} = \frac{8}{7} $$

   Cross-multiplying gives:

   $$ 18 \cdot 7 = 14 \cdot 8 $$

5. Calculate the Products

   Then perform the multiplication:

   $$ 126 = 112 $$

   Since this equation balances, we confirm the triangles are proportional.

6. Determine the Length x

   The last step is to find the length across the lake using similar triangles and their properties:

   $$ x = \frac{AB \cdot CD}{EB} = \frac{1800 \cdot 800}{1400} $$

   Calculate x:

   $$ x = \frac{1440000}{1400} = 1028.57 $$