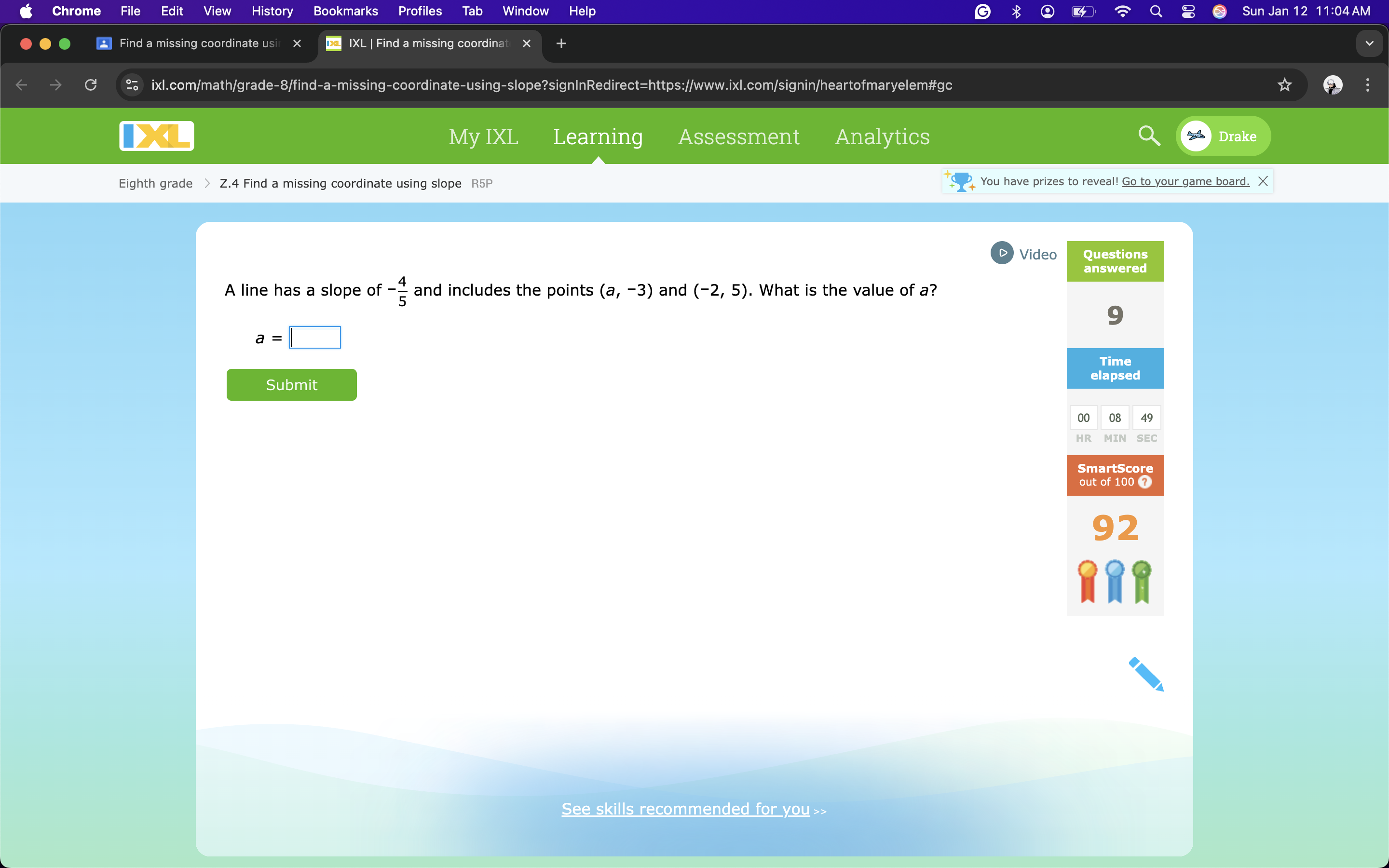
A line has a slope of -4/5 and includes the points (a, -3) and (-2, 5). What is the value of a?
Understand the Problem
The question is asking to find the missing x-coordinate 'a' of a point on a line with a given slope (-4/5) and a known point (-2, 5). We will use the slope formula to solve for 'a'.
Answer
The value of \( a \) is \( 8 \).
Answer for screen readers
The value of ( a ) is ( 8 ).
Steps to Solve
-
Identify the points and slope Given points are ( (a, -3) ) and ( (-2, 5) ), with a slope of ( m = -\frac{4}{5} ).
-
Use the slope formula The formula for slope ( m ) between two points ( (x_1, y_1) ) and ( (x_2, y_2) ) is: $$ m = \frac{y_2 - y_1}{x_2 - x_1} $$ Substituting the known values: $$ -\frac{4}{5} = \frac{5 - (-3)}{-2 - a} $$
-
Simplify the equation Simplifying the difference in the numerator gives: $$ 5 + 3 = 8 $$ So the equation now looks like: $$ -\frac{4}{5} = \frac{8}{-2 - a} $$
-
Cross-multiply to eliminate the fraction Cross-multiply to get rid of the fraction: $$ -4(-2 - a) = 5(8) $$
-
Distribute and solve for ( a ) Distributing gives: $$ 8 + 4a = 40 $$ Now, subtract 8 from both sides: $$ 4a = 32 $$ Next, divide by 4: $$ a = 8 $$
The value of ( a ) is ( 8 ).
More Information
We found the missing x-coordinate of the point on the line using the slope formula. The process involved substituting into the slope equation and solving for ( a ).
Tips
- Forgetting to simplify the slope equation before cross-multiplying.
- Neglecting to distribute correctly when cross-multiplying.
- Misreading the coordinates and mixing up ( x ) and ( y ) values.
AI-generated content may contain errors. Please verify critical information