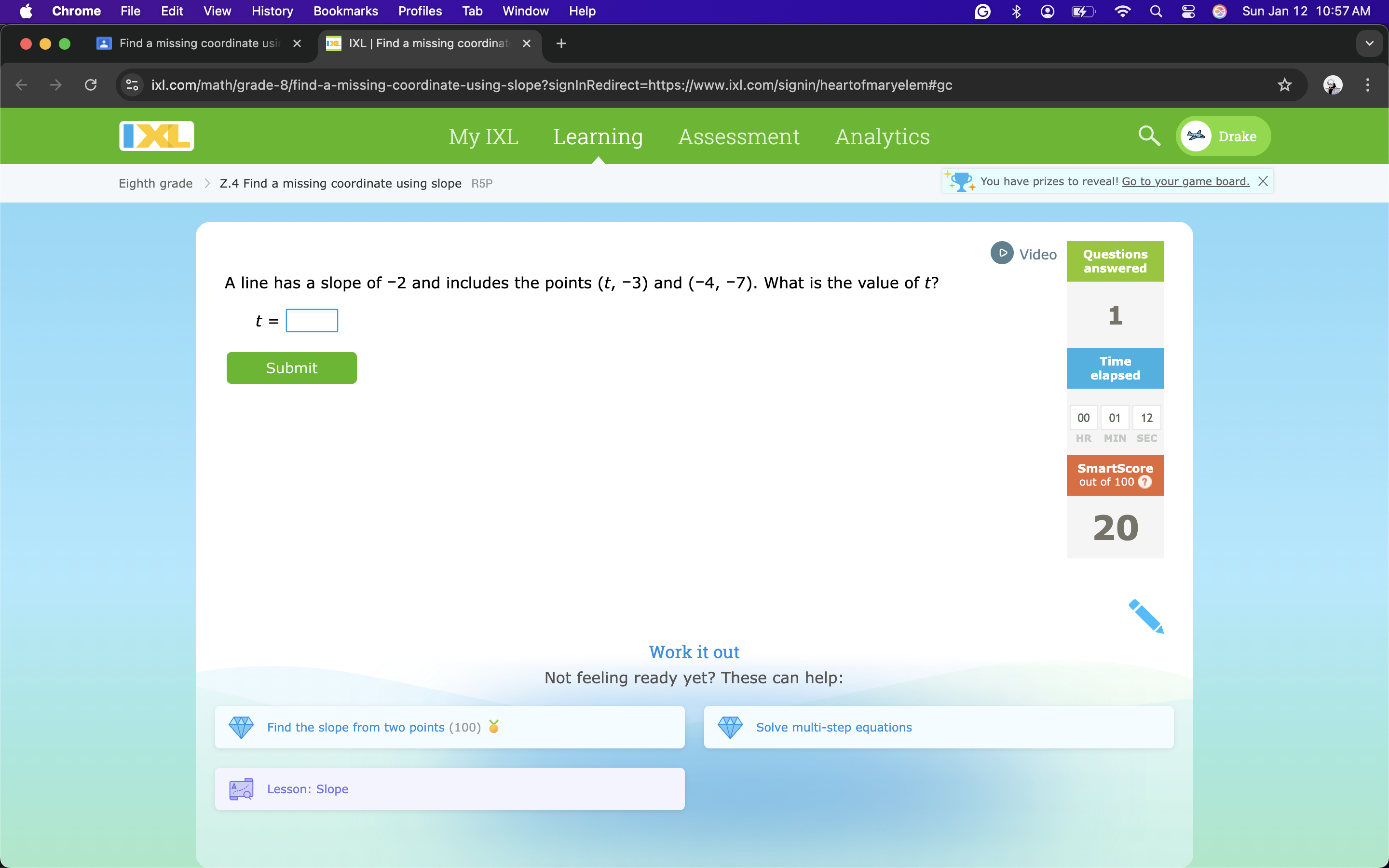
A line has a slope of -2 and includes the points (t, -3) and (-4, -7). What is the value of t?
Understand the Problem
The question is asking for the value of the variable 't' in the context of a line that has a defined slope of -2 and passes through the points (t, -3) and (-4, -7). To solve this, we can use the slope formula, which involves the coordinates of these points to find the unknown 't'.
Answer
The value of $t$ is $-6$.
Answer for screen readers
The value of $t$ is $-6$.
Steps to Solve
- Identify the slope formula
The slope of a line passing through two points $(x_1, y_1)$ and $(x_2, y_2)$ is calculated using the formula:
$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$
Here, we will use the given points $(t, -3)$ (Point 1) and $(-4, -7)$ (Point 2), and the slope $m$ is given as $-2$.
- Assign the values to the formula
We can assign the values as follows:
- Point 1: $(t, -3)$ → $x_1 = t$, $y_1 = -3$
- Point 2: $(-4, -7)$ → $x_2 = -4$, $y_2 = -7$
Substituting these into the slope formula gives us:
$$ -2 = \frac{-7 - (-3)}{-4 - t} $$
- Simplify the equation
First, simplify the numerator:
$$ -7 - (-3) = -7 + 3 = -4 $$
Thus, the equation now reads:
$$ -2 = \frac{-4}{-4 - t} $$
- Cross-multiply to eliminate the fraction
Cross-multiplying gives us:
$$ -2(-4 - t) = -4 $$
This simplifies to:
$$ 8 + 2t = -4 $$
- Solve for 't'
Now, rearranging the equation to isolate $t$:
$$ 2t = -4 - 8 $$
This simplifies to:
$$ 2t = -12 $$
Finally, dividing by 2:
$$ t = -6 $$
The value of $t$ is $-6$.
More Information
When dealing with slopes, it’s important to remember that the slope represents the steepness of a line. A negative slope, like $-2$, indicates the line descends as it moves from left to right.
Tips
- Forgetting to switch the signs when substituting values (e.g., incorrectly handling negative signs).
- Not simplifying the fraction properly before cross-multiplying.
- Miscalculating the final value of $t$ after simplifying the equation.
AI-generated content may contain errors. Please verify critical information