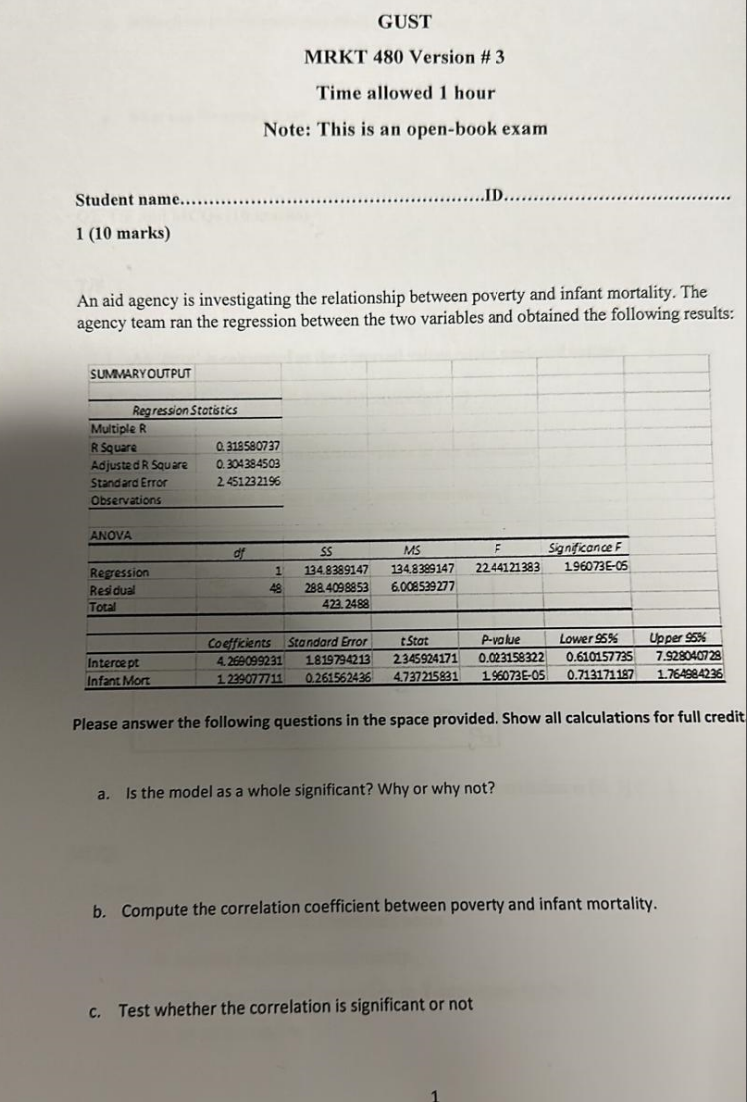
a. Is the model as a whole significant? Why or why not? b. Compute the correlation coefficient between poverty and infant mortality. c. Test whether the correlation is significant... a. Is the model as a whole significant? Why or why not? b. Compute the correlation coefficient between poverty and infant mortality. c. Test whether the correlation is significant or not.
Understand the Problem
The question is asking about the analysis of a regression model, specifically whether the model is significant as a whole, how to compute the correlation coefficient between poverty and infant mortality, and how to test the significance of that correlation. This involves statistical knowledge and an understanding of regression analysis.
Answer
The model is significant (p-value < 0.05), the correlation coefficient is $r \approx 0.3186$, and use the t-statistic for further correlation significance testing.
Answer for screen readers
a. Yes, the model is significant as a whole (p-value < 0.05).
b. The correlation coefficient between poverty and infant mortality is $r \approx 0.3186$.
c. To test correlation significance, use the t-statistic which is significant if the calculated value exceeds the critical t-value for $df = 420$.
Steps to Solve
- Determine Model Significance from ANOVA Table
To check if the model is significant, we can examine the F-statistic and its corresponding p-value from the ANOVA output.
- The F-statistic is $22.441 \text{ and the p-value is } 1.96073 \times 10^{-5}$.
Since the p-value is much less than the common significance level of 0.05, we conclude that the model is significant as a whole.
- Calculate the Correlation Coefficient
To find the correlation coefficient ($r$), we can use the following formula, where $R$ is the Multiple R value from the regression output.
- From the output, $R = 0.318580737$.
The correlation coefficient $r$ is equal to $R$:
$$ r = R = 0.3186 $$ (rounded to four decimal places)
- Test Significance of the Correlation Coefficient
We will use the t-statistic to test the significance of the correlation. The formula is:
$$ t = \frac{r \sqrt{n-2}}{\sqrt{1 - r^2}} $$
Here, $n$ is the number of observations, which is 422.
We will compute the t-statistic:
$$ t = \frac{0.3186 \sqrt{422-2}}{\sqrt{1 - (0.3186)^2}} $$
Calculate $t$:
- The degrees of freedom $df = n - 2 = 420$.
- The critical t-value for $df = 420$ and a significance level of 0.05 can be looked up using a t-table.
Using this calculation will allow us to determine the significance of the correlation.
a. Yes, the model is significant as a whole (p-value < 0.05).
b. The correlation coefficient between poverty and infant mortality is $r \approx 0.3186$.
c. To test correlation significance, use the t-statistic which is significant if the calculated value exceeds the critical t-value for $df = 420$.
More Information
This analysis indicates that there is a moderate positive correlation between poverty and infant mortality. A significant model means that the independent variable (poverty) effectively explains variations in the dependent variable (infant mortality).
Tips
- Confusing the correlation coefficient $r$ with the coefficient of determination $R^2$. Remember, $r$ represents the strength and direction of a linear relationship, while $R^2$ indicates how well the model explains the variability in the response variable.
- Misinterpreting the significance level; always check if the p-value is below 0.05 or your chosen alpha level when concluding significance.
AI-generated content may contain errors. Please verify critical information