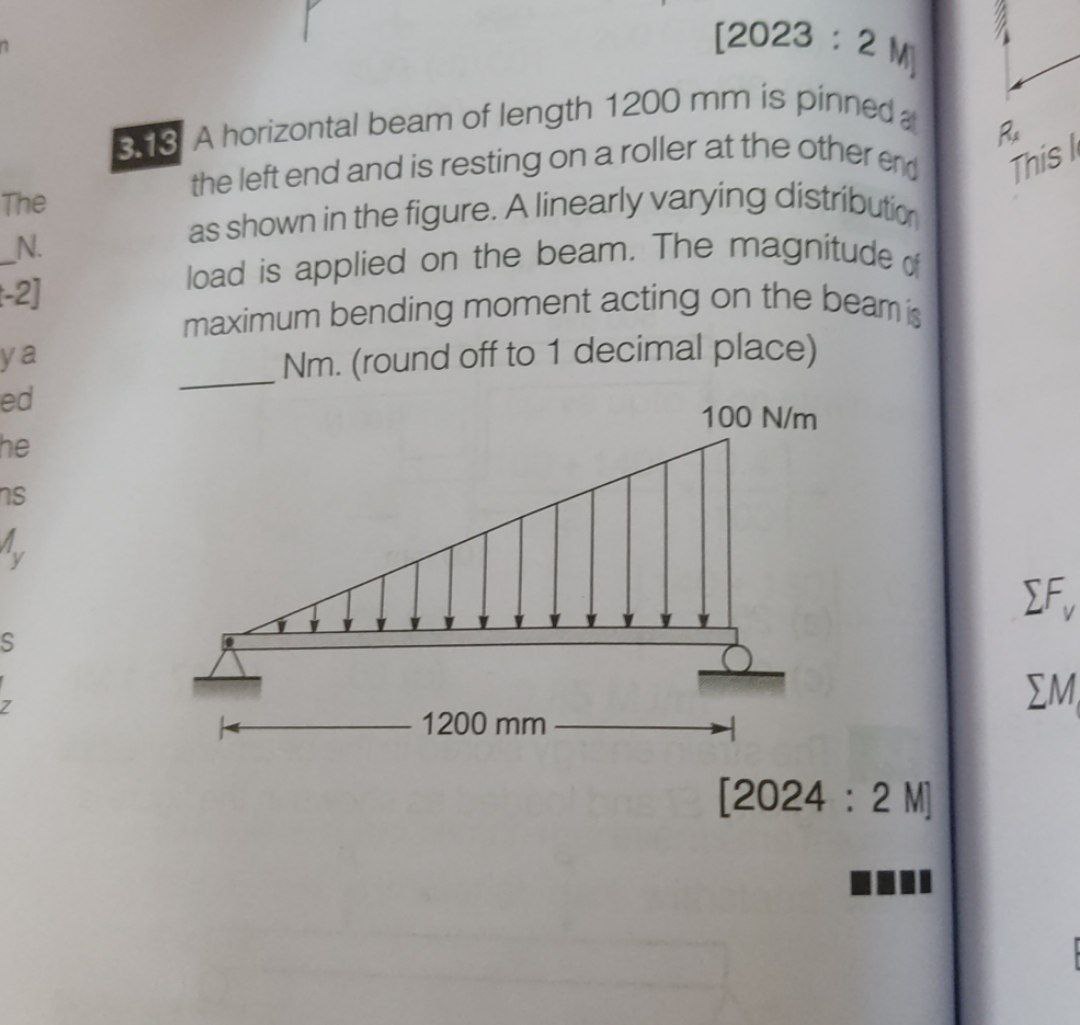
A horizontal beam of length 1200 mm is pinned at the left end and is resting on a roller at the other end. A linearly varying distribution load is applied on the beam. The magnitud... A horizontal beam of length 1200 mm is pinned at the left end and is resting on a roller at the other end. A linearly varying distribution load is applied on the beam. The magnitude of maximum bending moment acting on the beam is _____ Nm. (round off to 1 decimal place)
Understand the Problem
The question is asking to calculate the maximum bending moment acting on a horizontal beam subjected to a linearly varying distribution load. The beam length is given as 1200 mm, with a specific loading configuration shown in the figure. We need to find the bending moment and express it in Newton-meters, rounding off to one decimal place.
Answer
The magnitude of maximum bending moment acting on the beam is $48.0 \, \text{Nm}$.
Answer for screen readers
The magnitude of maximum bending moment acting on the beam is $48.0 , \text{Nm}$.
Steps to Solve
-
Identify Load Magnitude The maximum load intensity at the right end of the beam is $100 , \text{N/m}$, and since it is a linearly varying load, it ranges from $0 , \text{N/m}$ at the left end to $100 , \text{N/m}$ at the right end.
-
Calculate Total Load The total load $W$ can be calculated using the area of the triangular loading diagram: $$ W = \frac{1}{2} \times \text{base} \times \text{height} $$ Here, the base is the length of the beam ($1200 , \text{mm} = 1.2 , \text{m}$) and the height is the maximum intensity of the load ($100 , \text{N/m}$). $$ W = \frac{1}{2} \times 1.2 , \text{m} \times 100 , \text{N/m} = 60 , \text{N} $$
-
Determine Location of Resultant Load The resultant force acts at a distance of $\frac{1}{3}$ of the base from the larger end of the triangle. Thus: $$ \text{Location} = \frac{1.2 , \text{m}}{3} = 0.4 , \text{m} $$ from the right end (or $1.2 , \text{m} - 0.4 , \text{m} = 0.8 , \text{m}$ from the left end).
-
Calculate Support Reaction Forces Using static equilibrium, we can set up the moment about the left support (A): $$ \sum M_A = 0 \implies W \cdot 0.8 , \text{m} - R_B \cdot 1.2 , \text{m} = 0 $$ Where $R_B$ is the reaction at the right support. Solving for $R_B$: $$ R_B = \frac{W \cdot 0.8 , \text{m}}{1.2 , \text{m}} = \frac{60 \times 0.8}{1.2} = 40 , \text{N} $$
-
Calculate Maximum Bending Moment The maximum bending moment occurs at the fixed end (left support) due to the triangular load and can be calculated using: $$ M_{\text{max}} = \frac{1}{3} \times \text{load intensity} \times \text{length}^2 $$ Using the maximum intensity of load $100 , \text{N/m}$: $$ M_{\text{max}} = \frac{1}{3} \times 100 , \text{N/m} \times (1.2 , \text{m})^2 $$ $$ M_{\text{max}} = \frac{1}{3} \times 100 \times 1.44 = 48 , \text{Nm} $$
The magnitude of maximum bending moment acting on the beam is $48.0 , \text{Nm}$.
More Information
The bending moment provides a measure of the internal forces within a beam when subjected to loads. In this scenario, a linearly varying load results in a specific moment distribution along the beam, with the maximum occurring near the supports due to the nature of the load.
Tips
- Not calculating the resultant load correctly: It's essential to properly calculate the area under the loading diagram to determine the total force.
- Misplacing the resultant force: Ensure the resultant load location is calculated as $\frac{1}{3}$ of the triangle from the larger end.
- Incorrect moment balance: Always double-check equilibrium conditions for calculating reactions at supports.
AI-generated content may contain errors. Please verify critical information