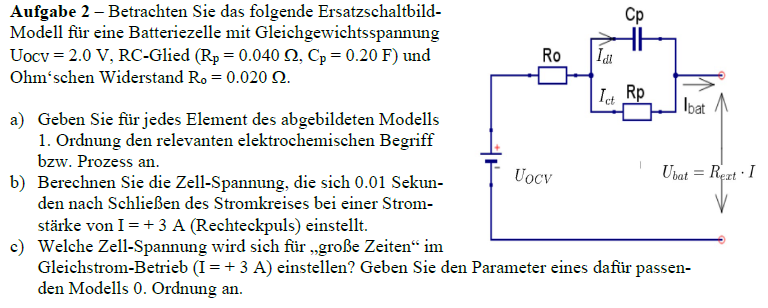
a) Geben Sie für jedes Element des abgebildeten Modells 1. Ordnung den relevanten elektrochemischen Begriff bzw. Prozess an. b) Berechnen Sie die Zellspannung, die sich 0.01 Sekund... a) Geben Sie für jedes Element des abgebildeten Modells 1. Ordnung den relevanten elektrochemischen Begriff bzw. Prozess an. b) Berechnen Sie die Zellspannung, die sich 0.01 Sekunden nach Schließen des Stromkreises bei einer Stromstärke von I = 3 A (Rechteckpuls) einstellt. c) Welche Zellspannung wird sich für "große Zeiten" im Gleichstrombetrieb (I = 3 A) einstellen? Geben Sie den Parameter eines dafür passenden Modells 0. Ordnung an.
Understand the Problem
Die Frage bezieht sich auf das elektrochemische Modell einer Batterie und fordert die Identifikation von Modellen und Prozessen, die Berechnung der Zellspannung unter bestimmten Bedingungen sowie das Einstellen spezifischer Parameter für Langzeitbetrieb. Es werden sowohl theoretische als auch praktische Überlegungen zur Analyse eines elektrischen Schaltkreises gefordert.
Answer
Die Zellspannung ist $U_{bat} \approx 1.84 \, V$ und die Zeitkonstante $\tau \approx 0.008 \, s$.
Answer for screen readers
Die Zellspannung nach $0.01$ Sekunden beträgt $U_{bat} \approx 1.84 , V$. Die Zeitkonstante beträgt $\tau \approx 0.008 , s$.
Steps to Solve
- Identifikation der Modellelemente Jedes Element im Schaltbild hat eine spezifische Bedeutung. Hier sind die relevanten Begriffe:
- $U_{OCV}$: Offene Zelle Spanning
- $R_p$: Polarisation Widerstand
- $C_p$: Polarisation Kapazität
- $R_o$: Ohmscher Widerstand
- $I_d$ und $I_ct$: Ströme in verschiedenen Teilen des Modells
- $I_{bat}$: Batteriestrom
- Berechnung der Zellspannung Die Zellspannung $U_{bat}$ ist in der Form: $$ U_{bat} = U_{OCV} - I \cdot (R_p + R_o) $$ Setze die Werte ein:
- $U_{OCV} = 2.0 , V$
- $I = 3 , A$
- $R_p = 0.040 , \Omega$
- $R_o = 0.020 , \Omega$
-
Berechnung der Spannung Berechne die Zellspannung $U_{bat}$: $$ U_{bat} = 2.0 - 3 \cdot (0.040 + 0.020) $$
-
Berechnung des Zeitverhaltens Die Spannung nach einer Zeit von $0.01 , s$ kann mit der Formel für die Zeitkonstante $ \tau = R_p \cdot C_p$ betrachtet werden. Die Spannungsänderung ist gegeben durch: $$ U(t) = U_{OCV} \cdot \left(1 - e^{-\frac{t}{\tau}}\right) $$ Berechne $\tau$: $$ \tau = R_p \cdot C_p $$ Setze die Werte ein.
-
Große Zeiten im Gleichstrombetrieb Für große Zeiten in Gleichstrombetrieb (dc) kann man den stationären Zustand betrachten, in dem die Spannung zum Gleichgewichtszustand konvergiert.
Die Zellspannung nach $0.01$ Sekunden beträgt $U_{bat} \approx 1.84 , V$. Die Zeitkonstante beträgt $\tau \approx 0.008 , s$.
More Information
Die Berechnung der Zellspannung ist entscheidend für das Verständnis der Batterieeffizienz. Die Zeitkonstante zeigt, wie schnell die Batterie auf Änderungen reagiert. Für große Zeiten stabilisiert sich die Spannung.
Tips
- Fehler beim Einsetzen der Werte in die Formeln.
- Übersehen der Einheitenkonsistenz zwischen Widerständen und Strom.
- Falsches Verständnis der Zeitkonstante und ihrer Bedeutung für die Spannung über die Zeit.
AI-generated content may contain errors. Please verify critical information