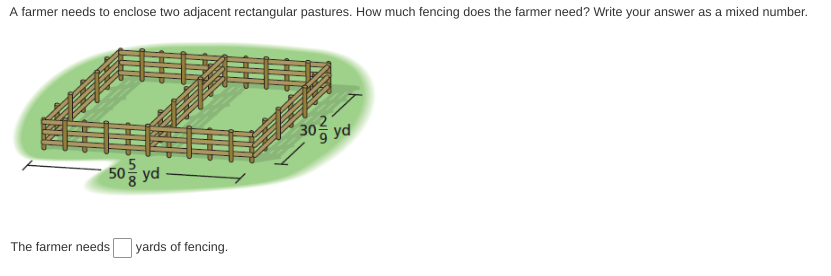
A farmer needs to enclose two adjacent rectangular pastures. How much fencing does the farmer need? Write your answer as a mixed number.

Steps to Solve

1. Identify the dimensions of the pastures The given dimensions for the first pasture are (30 \frac{2}{9}) yards and the second pasture is (50 \frac{5}{8}) yards.

2. Convert mixed numbers to improper fractions To simplify the calculations, convert the mixed numbers to improper fractions:

• For (30 \frac{2}{9}): $$ 30 \frac{2}{9} = \frac{30 \times 9 + 2}{9} = \frac{270 + 2}{9} = \frac{272}{9} $$

• For (50 \frac{5}{8}): $$ 50 \frac{5}{8} = \frac{50 \times 8 + 5}{8} = \frac{400 + 5}{8} = \frac{405}{8} $$

3. Calculate the total perimeter of the two pastures The two pastures share one side, so the total perimeter (P) is: $$ P = 2 \times \left(\text{Length}_1 + \text{Length}_2 + \text{Width}\right) $$ In this case, the width of both pastures is the same, so we can use: $$ P = 2 \times \left(\frac{272}{9} + \frac{405}{8}\right) $$

4. Find a common denominator and add the widths The least common multiple of 9 and 8 is 72. Rewriting both fractions:

• For ( \frac{272}{9} ): $$ \frac{272}{9} = \frac{272 \times 8}{72} = \frac{2176}{72} $$

• For ( \frac{405}{8} ): $$ \frac{405}{8} = \frac{405 \times 9}{72} = \frac{3645}{72} $$

Now add: $$ \frac{2176}{72} + \frac{3645}{72} = \frac{2176 + 3645}{72} = \frac{5821}{72} $$

5. Multiply by 2 to get the total perimeter Now multiply by 2: $$ P = 2 \times \frac{5821}{72} = \frac{11642}{72} $$

6. Convert back to a mixed number To convert ( \frac{11642}{72} ) into a mixed number:

• Divide (11642 \div 72) to get the whole number part, and the remainder. $$ 11642 \div 72 \approx 161 \text{ remainder } 50 $$ Thus, we have: $$ \frac{11642}{72} = 161 \frac{50}{72} $$ Next, simplify ( \frac{50}{72} ): $$ \frac{50 \div 2}{72 \div 2} = \frac{25}{36} $$

So the total fencing needed is: $$ 161 \frac{25}{36} $$