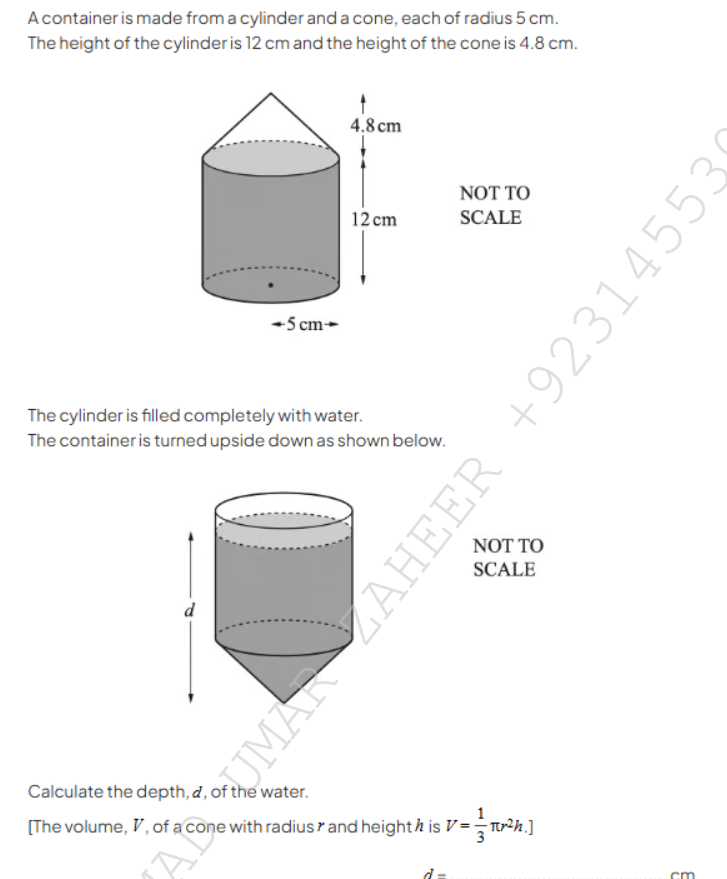
A container made from a cylinder and a cone, each radius 5 cm. The height of the cylinder is 12 cm and the height of the cone is 4.8 cm. The cylinder is filled completely with wate... A container made from a cylinder and a cone, each radius 5 cm. The height of the cylinder is 12 cm and the height of the cone is 4.8 cm. The cylinder is filled completely with water. After turning it upside down, calculate the depth, d, of the water. [The volume, V, of a cone with radius r and height h is V = 1/3 πr²h.] Read more

Steps to Solve

1. Calculate the total volume of water in the cylinder

The volume $V_c$ of the cylinder can be calculated using the formula:

$$ V_c = \pi r^2 h $$

Here, the radius $r = 5$ cm and the height $h = 12$ cm.

Substituting the values, we get:

$$ V_c = \pi (5)^2 (12) = 300\pi \text{ cm}^3 $$

2. Determine the volume of the cone

The volume $V_{cone}$ of the cone can be calculated using the formula:

$$ V_{cone} = \frac{1}{3} \pi r^2 h $$

For the cone, the radius $r = 5$ cm and the height $h = 4.8$ cm.

Substituting the values, we find:

$$ V_{cone} = \frac{1}{3} \pi (5)^2 (4.8) = 40 \pi \text{ cm}^3 $$

3. Set the volume of water equal to the volume of the cone

When the container is turned upside down, the water will fill the cone section. The depth $d$ of the water in the cone can be calculated by finding the relation between the volume of the water and the volume of the cone at that depth.

We can express the volume of water in the cone created by the water at depth $d$:

$$ V_{water} = \frac{1}{3} \pi r^2 d $$

Where $r$ is the radius at depth $d$. Considering the similar triangles, we can express the radius $r$ in terms of $d$:

$$ \frac{r}{d} = \frac{5}{4.8} \implies r = \frac{5}{4.8}d $$

Substituting this in the volume of water:

$$ V_{water} = \frac{1}{3} \pi \left(\frac{5}{4.8} d\right)^2 d $$

4. Equate the volumes

Setting the volume of water equal to the volume of the original cylindrical water:

$$ 300\pi = \frac{1}{3} \pi \left(\frac{5^2}{4.8^2}\right) d^3 $$

5. Simplify and solve for $d$

Cancel $\pi$ from both sides:

$$ 300 = \frac{1}{3} \left(\frac{25}{23.04}\right) d^3 $$

Multiply through by 3:

$$ 900 = \frac{25}{23.04} d^3 $$

Multiply through by $23.04$:

$$ 900 \times 23.04 = 25d^3 $$

Now divide by 25:

$$ d^3 = \frac{20736}{25} $$

Take the cube root of both sides:

$$ d = \sqrt[3]{829.44} $$

Calculating gives:

$$ d \approx 9.44 \text{ cm} $$