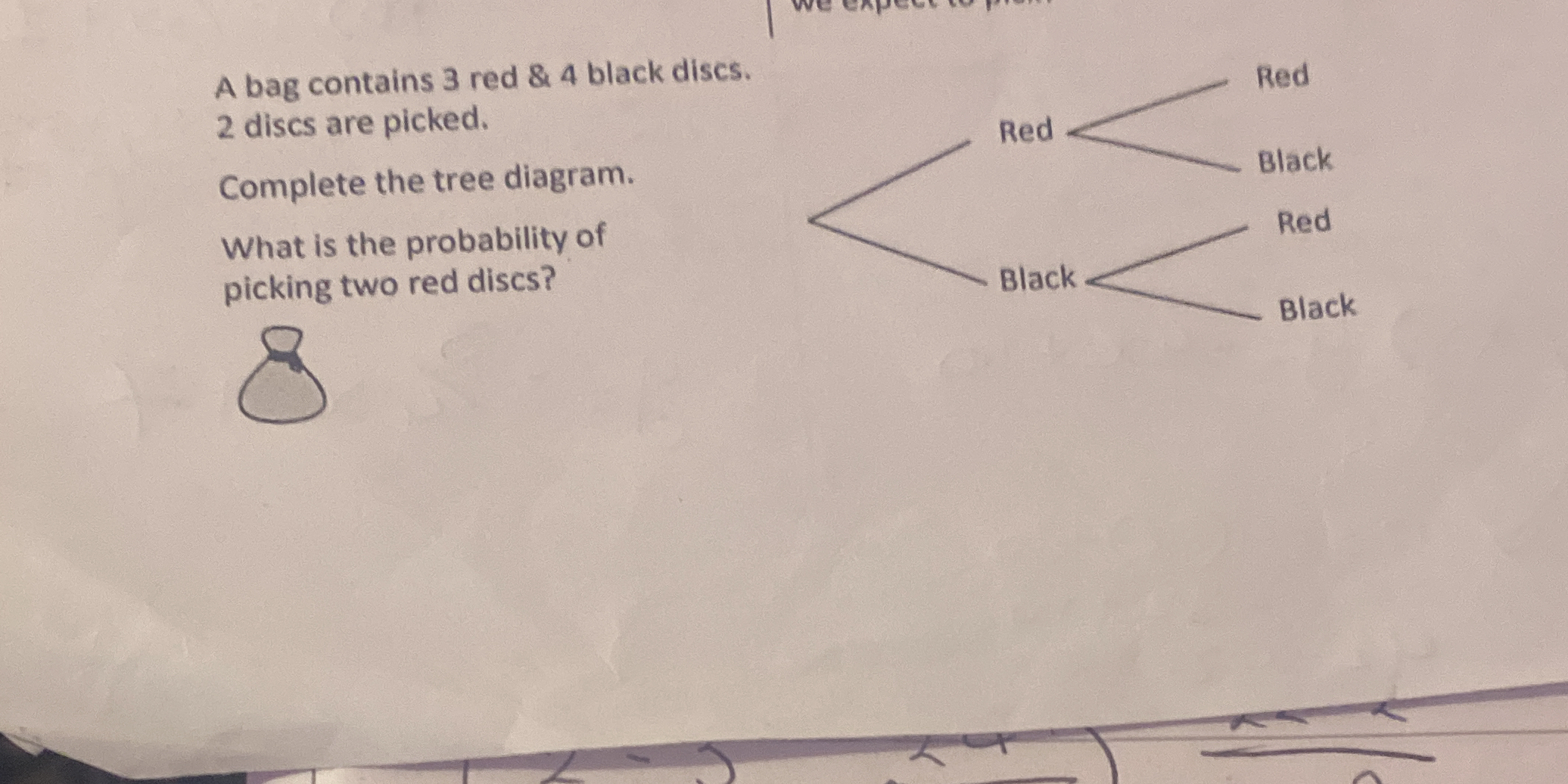
A bag contains 3 red & 4 black discs. 2 discs are picked. Complete the tree diagram. What is the probability of picking two red discs?

Steps to Solve

1. Identify Total Discs and Probabilities The bag contains 3 red discs and 4 black discs, making a total of 7 discs. We need to find the probabilities:

• Probability of picking a red disc first: $$ P(R) = \frac{3}{7} $$
• Probability of picking a black disc first: $$ P(B) = \frac{4}{7} $$

2. Calculate Probabilities for the Second Pick Next, we need to determine the probabilities for the second pick based on the first pick:

• If the first disc picked is red:

  • Remaining discs: 2 red, 4 black.
  • Probability of picking a red second: $$ P(R|R) = \frac{2}{6} = \frac{1}{3} $$

• If the first disc picked is black:

  • Remaining discs: 3 red, 3 black.
  • Probability of picking a red second: $$ P(R|B) = \frac{3}{6} = \frac{1}{2} $$

3. Construct the Tree Diagram Now we can draw the tree diagram:

                  Start
               /         \
           Red(3/7)     Black(4/7)
               / \           / \
      Red(1/3) Black(2/3) Red(1/2) Black(1/2)

4. Calculate the Probability of Both Picks Being Red To find the probability of picking two red discs:

• Using the probabilities from the tree: $$ P(R, R) = P(R) \cdot P(R|R) = \frac{3}{7} \cdot \frac{1}{3} = \frac{1}{7} $$

5. Summing Up Since there’s only one pathway to pick two red discs (i.e., red then red), this is the final probability.