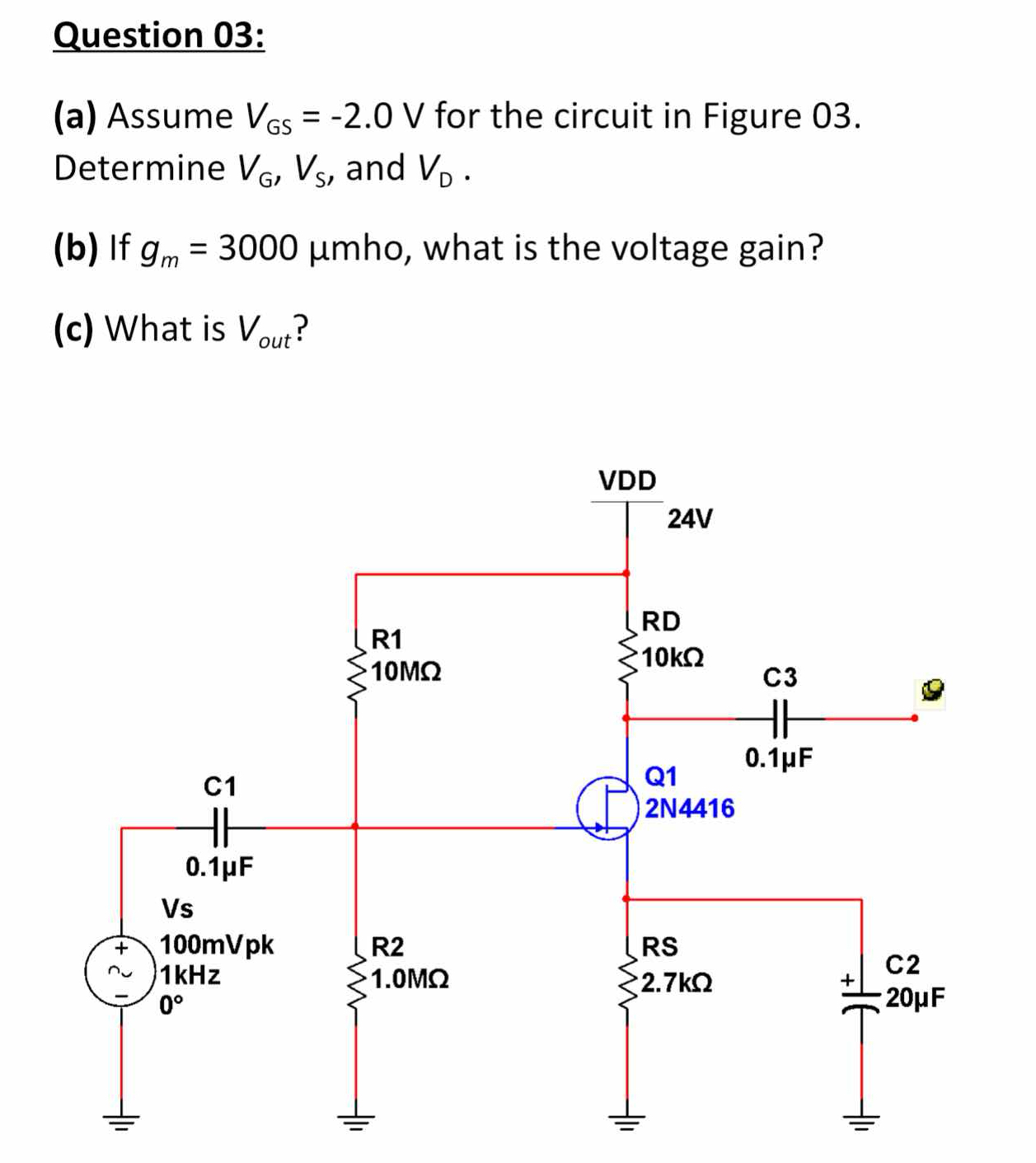
(a) Assume VGS = -2.0 V for the circuit in Figure 03. Determine VG, VS, and VD. (b) If gm = 3000 μmho, what is the voltage gain? (c) What is Vout?

Steps to Solve

1. Determine ( V_G )

To find ( V_G ), we use the voltage divider rule between resistors ( R_1 ) and ( R_2 ):

[ V_G = V_{DD} \cdot \frac{R_2}{R_1 + R_2} ]

Plugging in the values:

[ V_G = 24V \cdot \frac{1M\Omega}{10M\Omega + 1M\Omega} = 24V \cdot \frac{1}{11} \approx 2.18V ]

2. Determine ( V_S )

Since ( V_S ) is connected to the source of the transistor (Q1), we can express it as:

[ V_S = V_G - V_{GS} ]

Given ( V_{GS} = -2V ):

[ V_S = 2.18V - (-2V) = 2.18V + 2V = 4.18V ]

3. Determine ( V_D )

To find the drain voltage ( V_D ), we calculate the voltage across ( R_D ) using Ohm's law:

[ V_D = V_{DD} - I_D \cdot R_D ]

To find ( I_D), we can use:

[ I_D = g_m \cdot V_{GS} ]

With ( g_m = 3000 , \mu mho ) and ( V_{GS} = -2V ):

[ I_D = 3000 \times 10^{-6} \cdot (-2) = -0.006 , A ]

Calculating ( V_D):

[ V_D = 24V - (-0.006A) \cdot 10k\Omega = 24V + 60V = 84V \text{ (not possible; saturation)} ]

Instead, assuming saturation with ( V_D \approx V_S ):

[ V_D \approx 4.18V ]

4. Voltage Gain Calculation

For voltage gain ( A_V ):

[ A_V = -\frac{g_m \cdot R_D}{1 + g_m \cdot R_S} ]

Where ( R_S = 2.7k\Omega):

Calculating gain:

[ A_V = -\frac{3000 \times 10^{-6} \cdot 10k}{1 + (3000 \times 10^{-6} \cdot 2.7k)} = -\frac{30}{1 + 8.1} = -\frac{30}{9.1} \approx -3.30 ]

5. Determine ( V_{out} )

To find the output voltage ( V_{out} ):

[ V_{out} = A_V \cdot V_s = -3.30 \cdot 0.1V = -0.33V ]