Solve for x: 1 + (-x - 6) / 12 = 3 + (4 + 8x) / 28
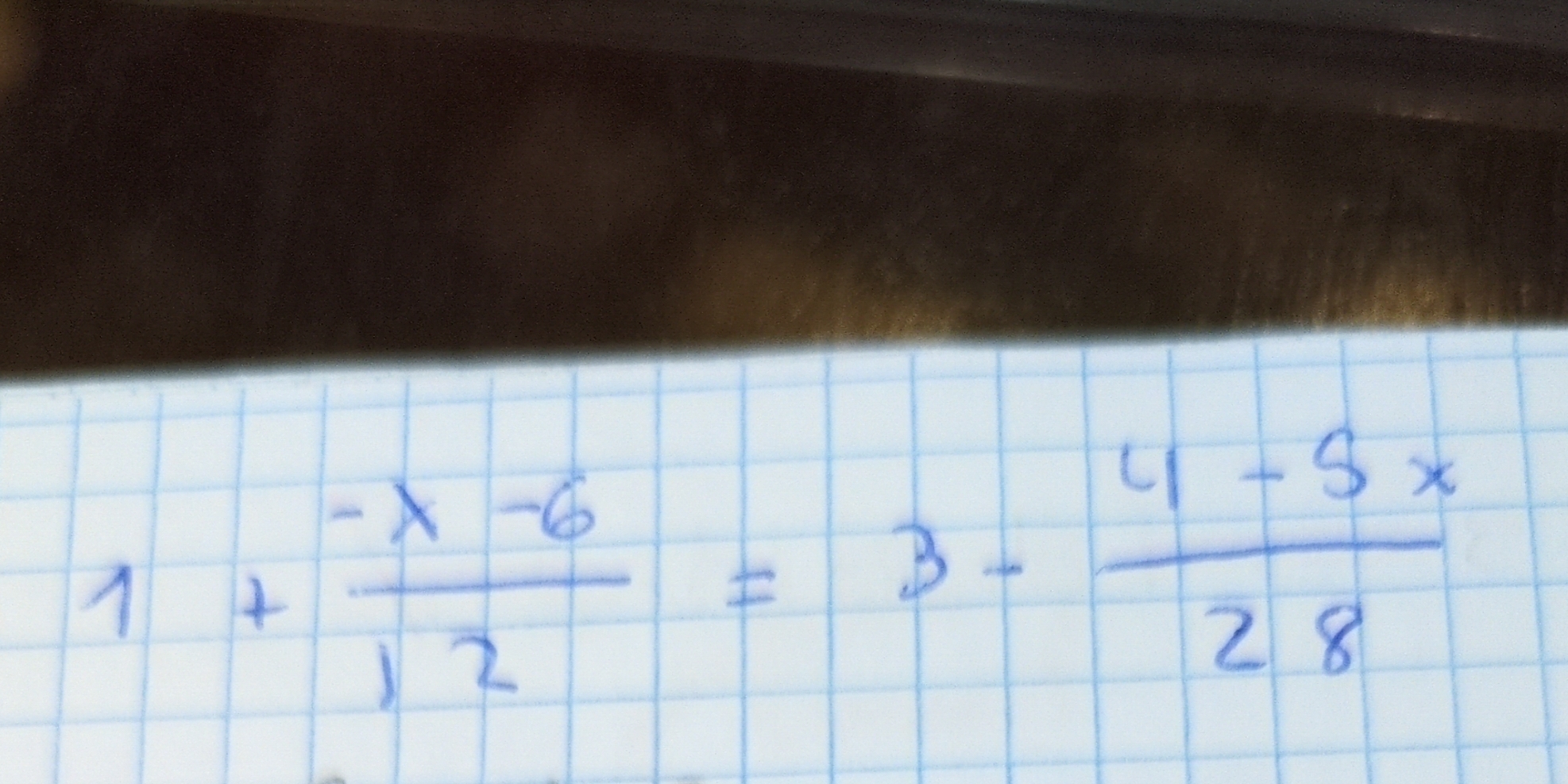
Understand the Problem
The question asks to solve for $x$ in the given linear equation. This will involve algebraic manipulation to isolate $x$ on one side of the equation.
Answer
$x = -\frac{222}{31}$
Answer for screen readers
$x = -\frac{222}{31}$
Steps to Solve
-
Rewrite the equation The given equation is $1 + \frac{-x - 6}{12} = 3 + \frac{4 + 8x}{28}$
-
Simplify the fractions Simplify the fraction $\frac{4 + 8x}{28}$ by dividing both numerator and denominator by 4. This gives $\frac{1+2x}{7}$. $1 + \frac{-x - 6}{12} = 3 + \frac{1 + 2x}{7}$
-
Eliminate fractions by multiplying by the least common multiple (LCM) The LCM of 12 and 7 is 84. Multiply both sides of the equation by 84. $84(1 + \frac{-x - 6}{12}) = 84(3 + \frac{1 + 2x}{7})$
-
Distribute and simplify Distribute the 84 on both sides: $84(1) + 84(\frac{-x - 6}{12}) = 84(3) + 84(\frac{1 + 2x}{7})$ $84 + 7(-x - 6) = 252 + 12(1 + 2x)$
-
Expand the parentheses $84 - 7x - 42 = 252 + 12 + 24x$
-
Combine like terms Combine the constants on the left side: $84 - 42 = 42$. Combine the constants on the right side: $252 + 12 = 264$. $42 - 7x = 264 + 24x$
-
Isolate x terms Add $7x$ to both sides: $42 - 7x + 7x = 264 + 24x + 7x$ $42 = 264 + 31x$
-
Isolate the constant terms Subtract 264 from both sides: $42 - 264 = 264 - 264 + 31x$ $-222 = 31x$
-
Solve for x Divide both sides by 31: $\frac{-222}{31} = \frac{31x}{31}$ $x = -\frac{222}{31}$ $x = - \frac{6 \times 37}{31}$
$x = -\frac{222}{31}$
More Information
The solution to the equation is $x = -\frac{222}{31}$, which is approximately -7.16.
Tips
A common mistake is not distributing correctly when multiplying by the LCM, especially with negative signs. Also, errors can occur when combining like terms. Another common mistake is not simplifying the fraction $\frac{4 + 8x}{28}$ before multiplying by the LCM.
AI-generated content may contain errors. Please verify critical information