7) (-1/2 + i)(2 - i/i) =
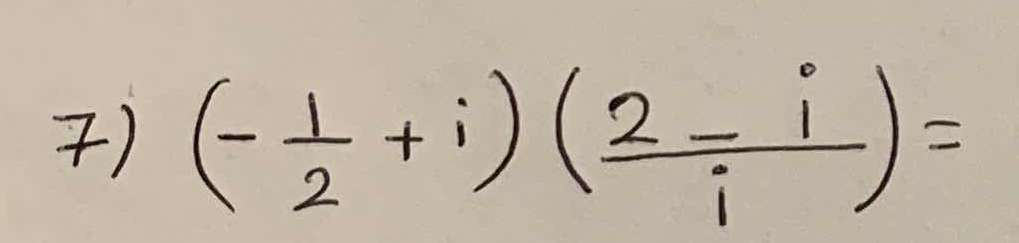
Understand the Problem
The question is asking to multiply two complex numbers, (-1/2 + i) and (2 - i/i), and simplify the result.
Answer
The answer is \( -\frac{5}{2} \).
Answer for screen readers
The result of multiplying the complex numbers is:
$$ -\frac{5}{2} $$
Steps to Solve
- Simplify the second complex number
First, simplify the expression ( \frac{2 - i}{i} ). Dividing by ( i ) can be done by multiplying the numerator and the denominator by ( -i ):
$$ \frac{2 - i}{i} = \frac{(2 - i)(-i)}{i(-i)} = \frac{-2i + i^2}{-1} = \frac{-2i - 1}{-1} = 2i + 1 $$
So, ( 2 - \frac{i}{i} = 1 + 2i ).
- Write the expression to multiply
Now we rewrite our expression to multiply: $$ (-\frac{1}{2} + i)(1 + 2i) $$
- Distribute the terms
Next, use the distributive property to multiply the terms:
$$ (-\frac{1}{2})(1) + (-\frac{1}{2})(2i) + (i)(1) + (i)(2i) $$
This simplifies to:
$$ -\frac{1}{2} - i + i + 2i^2 $$
- Substitute ( i^2 ) with (-1)
Remember that ( i^2 = -1 ). So we substitute:
$$ -\frac{1}{2} - i + i + 2(-1) = -\frac{1}{2} - 2 $$
- Combine like terms
Now combine the constant terms:
$$ -\frac{1}{2} - 2 = -\frac{1}{2} - \frac{4}{2} = -\frac{5}{2} $$
The result of multiplying the complex numbers is:
$$ -\frac{5}{2} $$
More Information
The final answer represents a complex number as a simplified real number. Multiplying complex numbers involves distributing each term and using the property ( i^2 = -1 ) to simplify.
Tips
- Forgetting to apply ( i^2 = -1 ) during simplification. Always remember this crucial identity.
- Not correctly simplifying complex expressions before multiplication. It's important to ensure all aspects of complex numbers are simplified first.
AI-generated content may contain errors. Please verify critical information