(4x + 1)(3x - 7) - (3x - 4)(z x - 8)

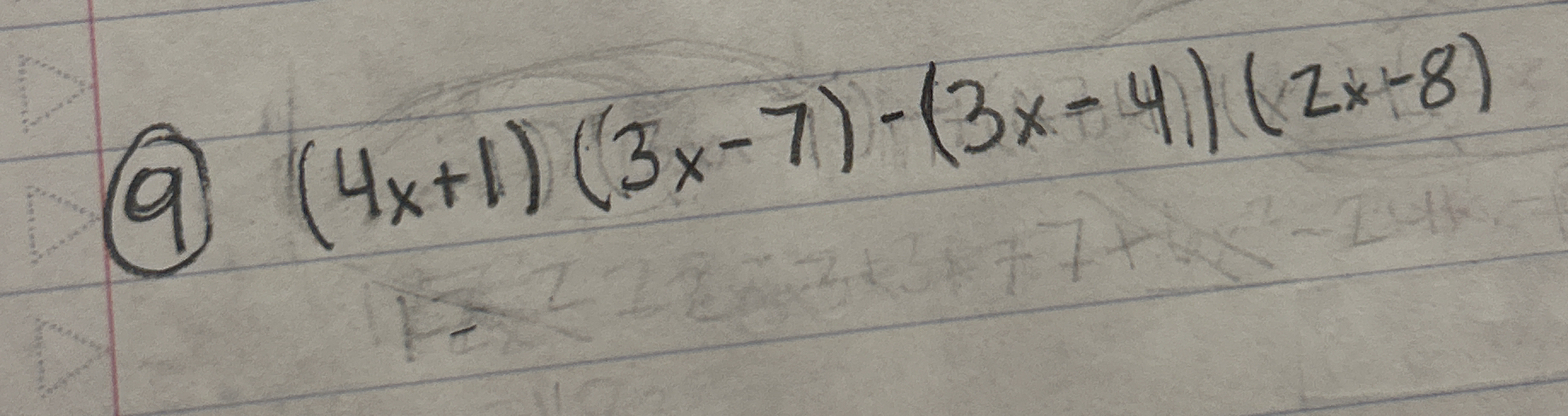
Understand the Problem

The question involves a mathematical expression that requires simplification or evaluation of the product and differences of polynomial expressions. We will use algebraic techniques like distribution to simplify the expression.

Answer

$$(12 - 3z)x^2 + (4z - 1)x - 39$$

Steps to Solve

First Expression Expansion

Expand the first part of the expression $(4x + 1)(3x - 7)$ using distribution: [ (4x)(3x) + (4x)(-7) + (1)(3x) + (1)(-7) ] This gives us: [ 12x^2 - 28x + 3x - 7 = 12x^2 - 25x - 7 ]

Second Expression Expansion

Now, expand the second part of the expression $(3x - 4)(zx - 8)$: [ (3x)(zx) + (3x)(-8) + (-4)(zx) + (-4)(-8) ] This becomes: [ 3zx^2 - 24x - 4zx + 32 = 3zx^2 - (4z + 24)x + 32 ]

Combine Both Expanded Results

Substitute the expanded results back into the original expression: [ (12x^2 - 25x - 7) - (3zx^2 - (4z + 24)x + 32) ]

Distribute Negative Sign

Distributing the negative sign: [ 12x^2 - 25x - 7 - 3zx^2 + (4z + 24)x - 32 ]

Combine Like Terms

Now combine like terms: [ (12 - 3z)x^2 + (-25 + 4z + 24)x + (-7 - 32) ] This simplifies to: [ (12 - 3z)x^2 + (4z - 1)x - 39 ]

The simplified expression is: $$(12 - 3z)x^2 + (4z - 1)x - 39$$

More Information

This expression represents a polynomial that combines the effects of both initial expressions. The coefficients are influenced by the parameters (z) and constants derived from the problem.

Tips

Forgetting to distribute the negative sign correctly can lead to incorrect signs in the terms.
Combining terms incorrectly can also cause mistakes; careful grouping of like terms is essential.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!