(4x + 1)(3x - 7) - (3x - 4)(2x - 8)
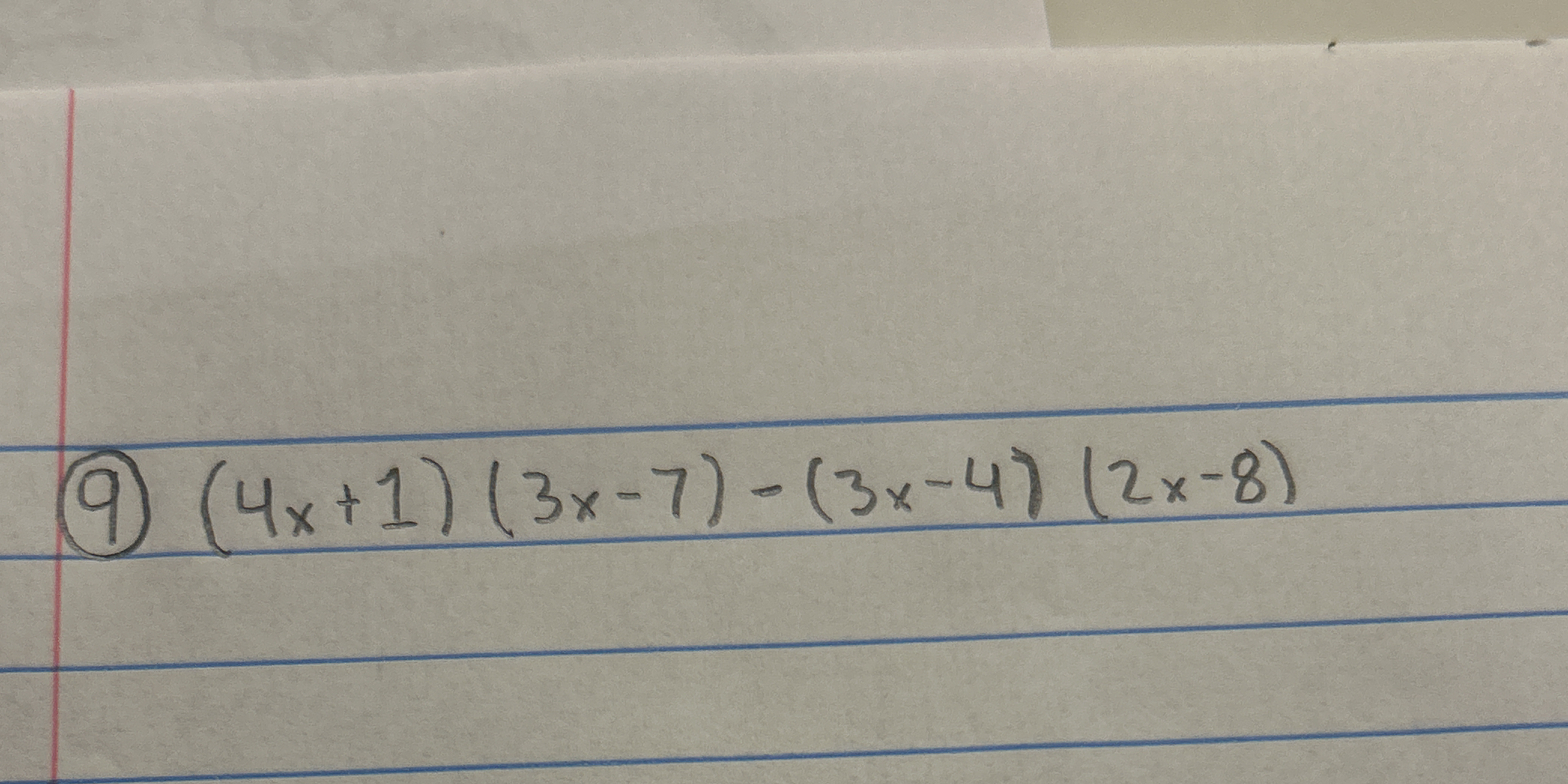
Understand the Problem
The question is asking to simplify the expression (4x + 1)(3x - 7) - (3x - 4)(2x - 8). This involves applying the distributive property to expand each part of the expression and then combining like terms.
Answer
The simplified expression is \( 6x^2 + 7x - 39 \).
Answer for screen readers
The simplified expression is ( 6x^2 + 7x - 39 ).
Steps to Solve
- Expand the first expression: (4x + 1)(3x - 7)
Using the distributive property (also known as the FOIL method for binomials):
$$ (4x + 1)(3x - 7) = 4x \cdot 3x + 4x \cdot (-7) + 1 \cdot 3x + 1 \cdot (-7) $$
Calculating each part:
- $4x \cdot 3x = 12x^2$
- $4x \cdot (-7) = -28x$
- $1 \cdot 3x = 3x$
- $1 \cdot (-7) = -7$
So, combining these gives:
$$ 12x^2 - 28x + 3x - 7 = 12x^2 - 25x - 7 $$
- Expand the second expression: (3x - 4)(2x - 8)
Again using the distributive property:
$$ (3x - 4)(2x - 8) = 3x \cdot 2x + 3x \cdot (-8) + (-4) \cdot 2x + (-4) \cdot (-8) $$
Calculating each part:
- $3x \cdot 2x = 6x^2$
- $3x \cdot (-8) = -24x$
- $-4 \cdot 2x = -8x$
- $-4 \cdot (-8) = 32$
So, combining these gives:
$$ 6x^2 - 24x - 8x + 32 = 6x^2 - 32x + 32 $$
- Subtract the second expression from the first
Now we combine the two expanded expressions from the previous steps:
$$ (12x^2 - 25x - 7) - (6x^2 - 32x + 32) $$
Distributing the negative sign:
$$ 12x^2 - 25x - 7 - 6x^2 + 32x - 32 $$
- Combine like terms
Combine the terms:
- For $x^2$ terms: $12x^2 - 6x^2 = 6x^2$
- For $x$ terms: $-25x + 32x = 7x$
- For constant terms: $-7 - 32 = -39$
So, putting them all together gives:
$$ 6x^2 + 7x - 39 $$
The simplified expression is ( 6x^2 + 7x - 39 ).
More Information
This expression represents a quadratic polynomial, which can be graphed as a parabola. Quadratic functions have various applications, including physics for describing projectile motion.
Tips
- Forgetting to distribute the negative sign: When subtracting the second expression, it's crucial to distribute the negative sign to all terms.
- Combining like terms incorrectly: Ensure that only like terms are combined together.
AI-generated content may contain errors. Please verify critical information