4√72 - 4√18 + √200

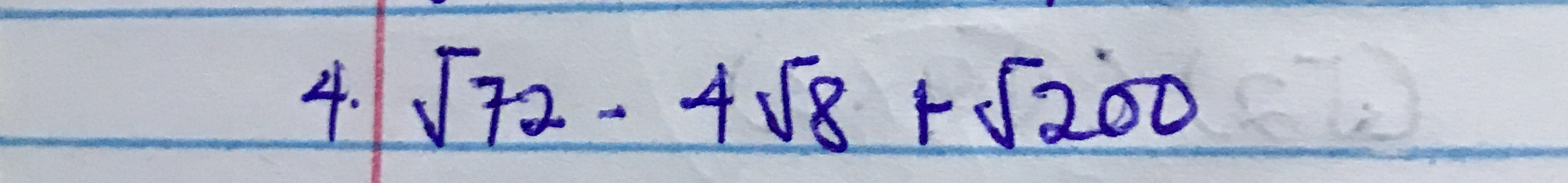
Understand the Problem

The question involves simplifying the expression with square roots: 4√72 - 4√18 + √200. We will simplify each square root and combine like terms.

Answer

The simplified expression is $ 22\sqrt{2} $.

Steps to Solve

Simplify each square root individually

Start by simplifying the square roots in the expression:
- For $\sqrt{72}$: $$ \sqrt{72} = \sqrt{36 \cdot 2} = \sqrt{36} \cdot \sqrt{2} = 6\sqrt{2} $$
- For $\sqrt{18}$: $$ \sqrt{18} = \sqrt{9 \cdot 2} = \sqrt{9} \cdot \sqrt{2} = 3\sqrt{2} $$
- For $\sqrt{200}$: $$ \sqrt{200} = \sqrt{100 \cdot 2} = \sqrt{100} \cdot \sqrt{2} = 10\sqrt{2} $$
Substitute the simplified square roots back into the expression

Replace the simplified square roots in the original expression: $$ 4\sqrt{72} - 4\sqrt{18} + \sqrt{200} $$ becomes: $$ 4(6\sqrt{2}) - 4(3\sqrt{2}) + 10\sqrt{2} $$
Simplify using distribution

Now distribute the coefficients:
- For $4(6\sqrt{2})$: $$ 24\sqrt{2} $$
- For $4(3\sqrt{2})$: $$ 12\sqrt{2} $$
So the expression is now: $$ 24\sqrt{2} - 12\sqrt{2} + 10\sqrt{2} $$
Combine like terms

Add and subtract the coefficients of $\sqrt{2}$: $$ (24 - 12 + 10)\sqrt{2} = 22\sqrt{2} $$

The final simplified expression is ( 22\sqrt{2} ).

More Information

This process highlights how simplifying square roots can make it easier to manage and combine terms in algebraic expressions. Knowing how to factor and simplify square roots is a valuable skill in math.

Tips

Forgetting to simplify the square roots before combining terms.
Neglecting to apply the correct signs when combining like terms, which can lead to errors in the final result.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!