3a + 4b - (4a + b)
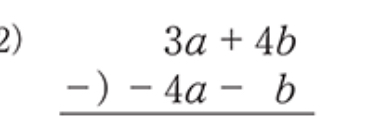
Understand the Problem
The question is asking us to simplify the expression by subtracting the second polynomial from the first one, which involves combining like terms.
Answer
The simplified expression is $$ -a + 3b $$.
Answer for screen readers
The simplified expression is:
$$ -a + 3b $$
Steps to Solve
-
Distribute the negative sign
Distributing the negative sign across the second polynomial means we will change the signs of each term.
Starting expression:
$$ 3a + 4b - (4a + b) $$
This simplifies to:
$$ 3a + 4b - 4a - b $$ -
Combine like terms for 'a'
Now, we group the terms involving 'a'.
From the previous step, we have:
$$ (3a - 4a) + (4b - b) $$
This simplifies to:
$$ -1a + 4b $$ or $$ -a + 4b $$ -
Combine like terms for 'b'
Next, we combine the terms involving 'b':
Continuing from the previous equation:
$$ -a + (4b - 1b) $$
This simplifies to:
$$ -a + 3b $$
The simplified expression is:
$$ -a + 3b $$
More Information
The operation we performed is a common algebraic technique known as combining like terms, which is essential for simplifying algebraic expressions. It's important when handling polynomials to pay attention to the signs and ensure accurate distribution.
Tips
- Forgetting to distribute the negative sign correctly when subtracting polynomials.
- Miscalculating the coefficients of like terms during the combination process.
AI-generated content may contain errors. Please verify critical information