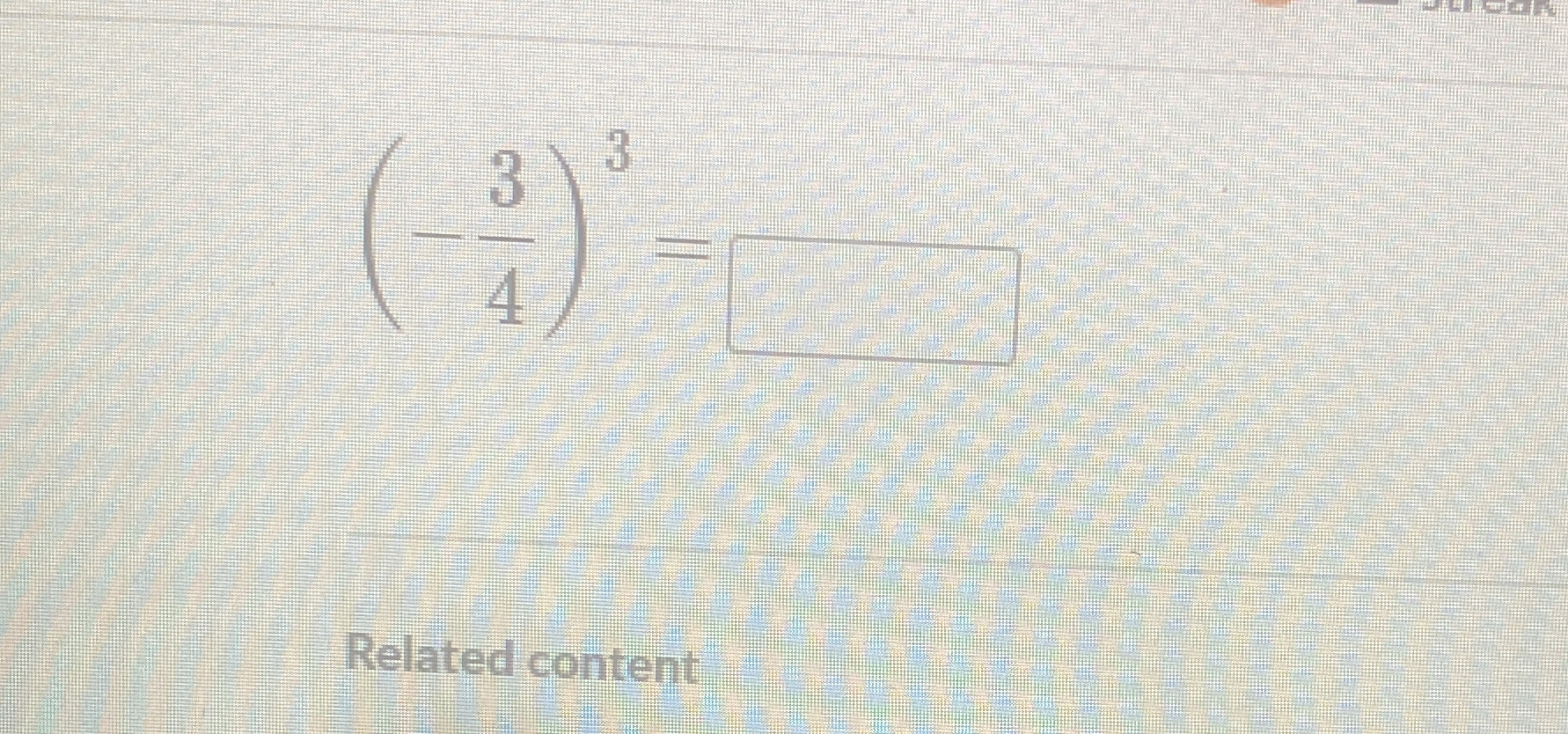
(3/4)^3 =
Understand the Problem
The question is asking to solve the mathematical expression (3/4)^3, which involves calculating the cube of the fraction 3/4.
Answer
The answer is \(\frac{27}{64}\).
Answer for screen readers
The final answer is (\frac{27}{64}).
Steps to Solve
-
Understand the expression We need to calculate the cube of the fraction (\frac{3}{4}).
-
Use the power of a fraction rule When raising a fraction to a power, both the numerator and the denominator are raised to that power. Therefore, we have:
$$ \left(\frac{3}{4}\right)^3 = \frac{3^3}{4^3} $$
-
Calculate the numerator Calculate (3^3):
$$ 3^3 = 3 \times 3 \times 3 = 27 $$
-
Calculate the denominator Calculate (4^3):
$$ 4^3 = 4 \times 4 \times 4 = 64 $$
-
Combine the results The expression can now be written as:
$$ \left(\frac{3}{4}\right)^3 = \frac{27}{64} $$
The final answer is (\frac{27}{64}).
More Information
Cubing a fraction involves cubing both the numerator and the denominator separately. This is an important concept in exponential operations involving fractions.
Tips
- A common mistake is to only cube one part of the fraction and forget to cube the other part.
- Another mistake is to miscalculate either (3^3) or (4^3). Always double-check calculations for accuracy.
AI-generated content may contain errors. Please verify critical information