3/4(1/2 x + 2/3) + 1/4 x = 6 3/4
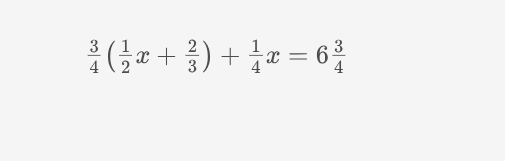
Understand the Problem
The question is asking to solve the equation involving variables and fractions. We will simplify the equation step-by-step to find the value of 'x'.
Answer
The value of \( x \) is \( 10 \).
Answer for screen readers
The value of ( x ) is ( 10 ).
Steps to Solve
-
Convert the mixed number to an improper fraction
To solve the equation, first convert ( 6\frac{3}{4} ) into an improper fraction:
$$ 6\frac{3}{4} = \frac{6 \times 4 + 3}{4} = \frac{24 + 3}{4} = \frac{27}{4} $$ -
Distribute the fraction
Now distribute ( \frac{3}{4} ) inside the parentheses:
$$ \frac{3}{4} \left( \frac{1}{2} x + \frac{2}{3} \right) = \frac{3}{4} \cdot \frac{1}{2} x + \frac{3}{4} \cdot \frac{2}{3} $$
Calculate the terms separately:
$$ \frac{3}{4} \cdot \frac{1}{2} x = \frac{3}{8} x $$
$$ \frac{3}{4} \cdot \frac{2}{3} = \frac{3 \cdot 2}{4 \cdot 3} = \frac{2}{4} = \frac{1}{2} $$
So, the equation now is:
$$ \frac{3}{8} x + \frac{1}{2} + \frac{1}{4} x = \frac{27}{4} $$ -
Combine like terms
Now combine ( \frac{3}{8} x ) and ( \frac{1}{4} x ):
Convert ( \frac{1}{4} x ) to eighths:
$$ \frac{1}{4} x = \frac{2}{8} x $$
Now we can add them:
$$ \frac{3}{8} x + \frac{2}{8} x = \frac{5}{8} x $$
The equation simplifies to:
$$ \frac{5}{8} x + \frac{1}{2} = \frac{27}{4} $$ -
Isolate the term with x
Subtract ( \frac{1}{2} ) from both sides of the equation:
Convert ( \frac{1}{2} ) to fourths:
$$ \frac{1}{2} = \frac{2}{4} $$
So,
$$ \frac{27}{4} - \frac{2}{4} = \frac{25}{4} $$
This gives us:
$$ \frac{5}{8} x = \frac{25}{4} $$ -
Solve for x
Multiply both sides by the reciprocal of ( \frac{5}{8} ):
$$ \frac{8}{5} \cdot \frac{5}{8} x = \frac{8}{5} \cdot \frac{25}{4} $$
So, $x$ simplifies to:
$$ x = \frac{8 \cdot 25}{5 \cdot 4} = \frac{200}{20} = 10 $$
The value of ( x ) is ( 10 ).
More Information
In this problem, we used distribution and fraction operations to isolate the variable ( x ). This type of equation is common in algebra, often leading to the use of mixed numbers and improper fractions.
Tips
- Failing to properly distribute the fraction to both terms inside the parentheses.
- Not converting mixed numbers to improper fractions correctly.
- Confusing addition of fractions—be careful to have a common denominator when combining fractions.
AI-generated content may contain errors. Please verify critical information