2r^5 x 3r^2 x 4r^3
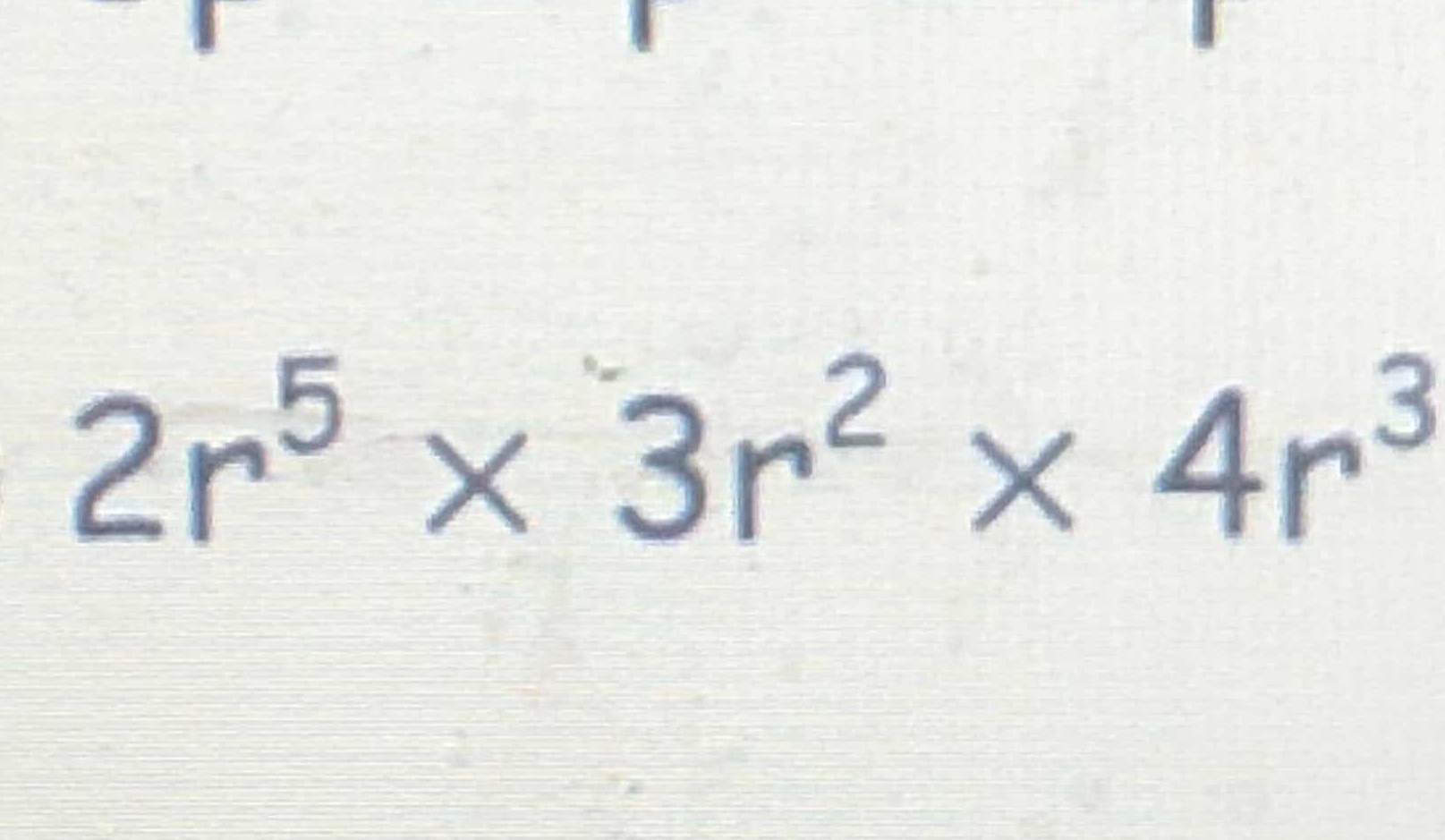
Understand the Problem
The question is asking for the multiplication of the algebraic terms presented, which includes coefficients and variables raised to certain powers.
Answer
$24r^{10}$
Answer for screen readers
The final answer is $24r^{10}$.
Steps to Solve
-
Multiply the coefficients Multiply the numerical coefficients from each term: $$ 2 \times 3 \times 4 $$ This gives us: $$ 2 \times 3 = 6 $$ Then: $$ 6 \times 4 = 24 $$
-
Add the exponents Now, we will add the exponents of the variable ( r ) using the property ( r^a \times r^b = r^{a+b} ): $$ r^5 \times r^2 \times r^3 $$ Adding the exponents: $$ 5 + 2 + 3 = 10 $$ This gives us: $$ r^{10} $$
-
Combine results Now combine the results from the coefficients and the variable terms: $$ 24r^{10} $$
The final answer is $24r^{10}$.
More Information
When multiplying algebraic expressions, remember to separately address the coefficients and the variables. The process of adding exponents holds true as long as the bases (in this case, the variable ( r )) are the same.
Tips
- Forgetting to add the exponents of the same bases.
- Mistaking the multiplication of coefficients as addition. Always multiply numerical terms.
AI-generated content may contain errors. Please verify critical information