2/9 - 1/5
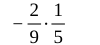
Understand the Problem
The question involves performing mathematical operations, specifically involving fractions in a subtraction and multiplication format. We will solve the equation step by step.
Answer
The answer is \( \frac{1}{45} \).
Answer for screen readers
The final answer is ( \frac{1}{45} ).
Steps to Solve
- Identify the fractions involved
The equation given is ( \frac{2}{9} - \frac{1}{5} ).
- Find a common denominator
The denominators are 9 and 5. The least common multiple (LCM) of 9 and 5 is 45.
- Rewrite the fractions with the common denominator
Convert each fraction:
-
For ( \frac{2}{9} ): $$ \frac{2}{9} = \frac{2 \times 5}{9 \times 5} = \frac{10}{45} $$
-
For ( \frac{1}{5} ): $$ \frac{1}{5} = \frac{1 \times 9}{5 \times 9} = \frac{9}{45} $$
- Subtract the fractions
Now subtract the two fractions: $$ \frac{10}{45} - \frac{9}{45} = \frac{10 - 9}{45} = \frac{1}{45} $$
The final answer is ( \frac{1}{45} ).
More Information
Subtracting fractions requires a common denominator, and understanding how to convert fractions to equivalent forms is crucial for solving these types of problems. The least common multiple (LCM) is essential when dealing with different denominators.
Tips
- Not finding the correct common denominator. Always ensure you find the LCM of the denominators.
- Failing to convert both fractions properly before subtraction. It's essential to rewrite each fraction with the common denominator.
AI-generated content may contain errors. Please verify critical information