14x - 3y + √(12 + √(12 + √(12 + ...)))

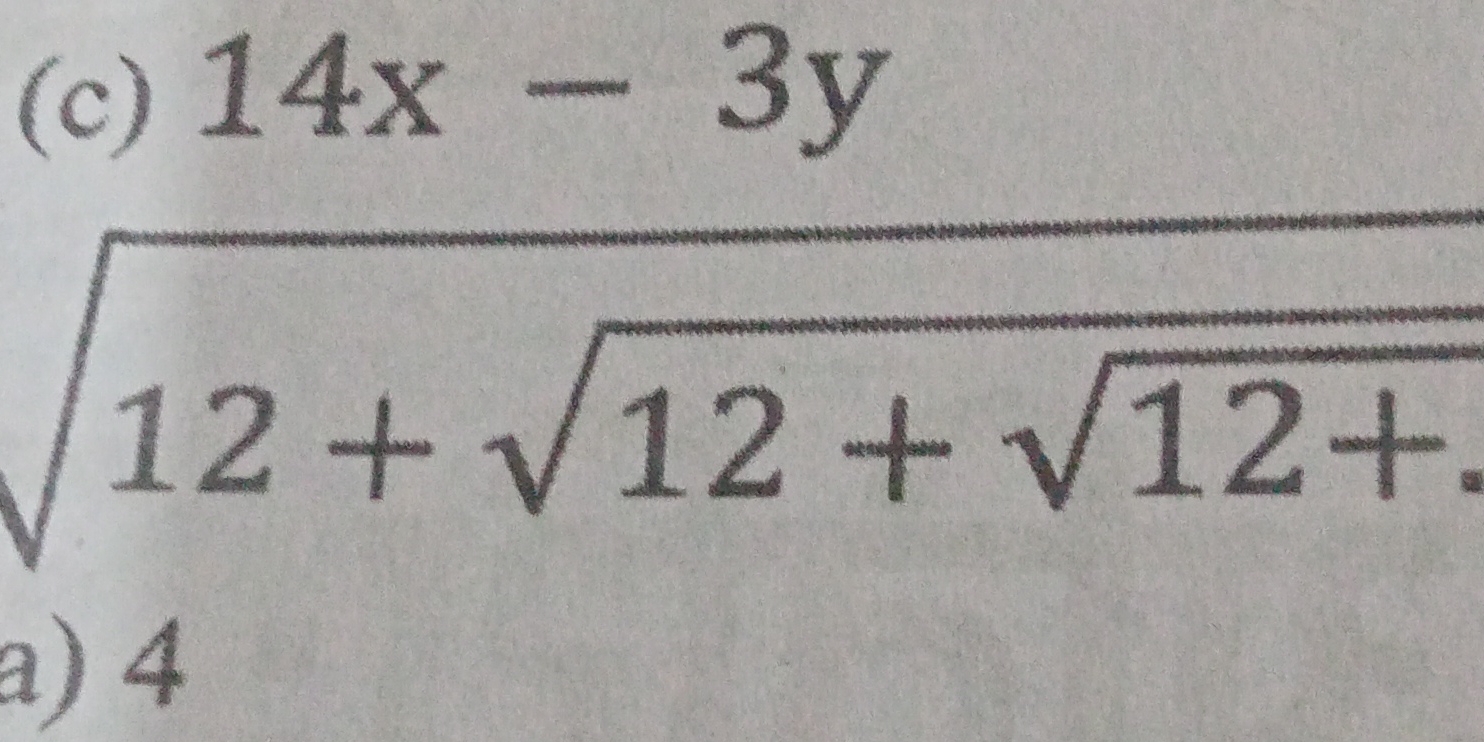
Understand the Problem

The question is presenting an expression involving square roots and variables, and it seems to require simplification or solving for given variables.

Answer

The expression simplifies to $ 60 - 3y $.

Steps to Solve

Set up the equation for the square root expression

Let $x = \sqrt{12 + \sqrt{12 + \sqrt{12 + \ldots}}}$.

This means we can rewrite the expression as:

$$ x = \sqrt{12 + x} $$

Square both sides of the equation

To eliminate the square root, we'll square both sides:

$$ x^2 = 12 + x $$

Rearrange the equation

Rearranging gives us a standard form quadratic equation:

$$ x^2 - x - 12 = 0 $$

Factor the quadratic equation

Next, we need to factor the quadratic. We look for two numbers that multiply to -12 and add to -1. The factors are -4 and 3. Thus we can factor it as:

$$(x - 4)(x + 3) = 0 $$

Solve for x

Setting each factor to zero gives:

$$ x - 4 = 0 \quad \Rightarrow \quad x = 4 $$

$$ x + 3 = 0 \quad \Rightarrow \quad x = -3 $$

Since $x$ must be positive (as it represents a square root), we choose:

$$ x = 4 $$

Plug back into the original expression

Now substitute $x$ back into the original expression to get the final answer:

$$ 14x - 3y + x = 14(4) - 3y + 4 $$

This simplifies to:

$$ 56 - 3y + 4 = 60 - 3y $$

The expression simplifies to ( 60 - 3y ).

More Information

The original square root expression converges to 4 because of its self-similar structure. This is a classic example of evaluating an infinite nested radical.

Tips

Forgetting to square both sides correctly when isolating the variable.
Disregarding the fact that the result from a square root must be non-negative, leading to rejecting a negative solution.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!