(-1/2 + i)(2 - i)/i =
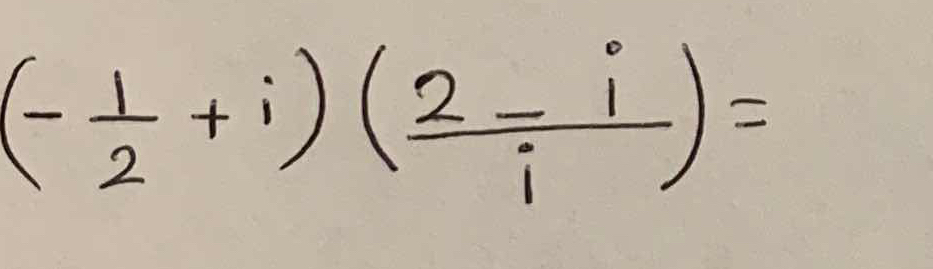
Understand the Problem
The question asks for the result of multiplying two complex numbers: (-1/2 + i) and (2 - i)/i. To solve it, we would first simplify (2 - i)/i and then multiply the resulting complex number with (-1/2 + i).
Answer
The result of the multiplication is \( \frac{5}{2} \).
Answer for screen readers
The final answer is ( \frac{5}{2} ).
Steps to Solve
- Simplify the division of complex numbers
To simplify the expression ( \frac{2 - i}{i} ), we can multiply both the numerator and the denominator by ( i ) to eliminate the imaginary unit in the denominator:
$$ \frac{(2 - i) \cdot i}{i \cdot i} = \frac{2i - i^2}{-1} = - (2i + 1) = -1 - 2i $$
- Multiply the first complex number by the simplified one
Now we will multiply the two complex numbers: ( (-\frac{1}{2} + i) ) and ( (-1 - 2i) ).
Using the distributive property:
$$ (-\frac{1}{2} + i)(-1 - 2i) = -\frac{1}{2} \cdot (-1) + -\frac{1}{2} \cdot (-2i) + i \cdot (-1) + i \cdot (-2i) $$
- Calculate each term
Calculating each term:
-
The first term: $$ -\frac{1}{2} \cdot (-1) = \frac{1}{2} $$
-
The second term: $$ -\frac{1}{2} \cdot (-2i) = i $$
-
The third term: $$ i \cdot (-1) = -i $$
-
The fourth term (note that ( i^2 = -1 )): $$ i \cdot (-2i) = -2(-1) = 2 $$
- Combine the results
Adding these together gives:
$$ \frac{1}{2} + i - i + 2 = \frac{1}{2} + 2 = \frac{5}{2} $$
So, the final result is:
$$ \frac{5}{2} $$
The final answer is ( \frac{5}{2} ).
More Information
The answer represents the product of two complex numbers after simplifying and multiplying them. Multiplication of complex numbers involves both the real and imaginary components, and it's important to remember that ( i^2 = -1 ).
Tips
- Forgetting to multiply by ( i ) when simplifying ( \frac{2 - i}{i} ).
- Overlooking the negative signs while distributing when multiplying complex numbers.
- Not combining like terms correctly after multiplication.
AI-generated content may contain errors. Please verify critical information