1^2 + 2^2 + 3^2 + ... + n^2 = n(n+1)(2n+1)/6

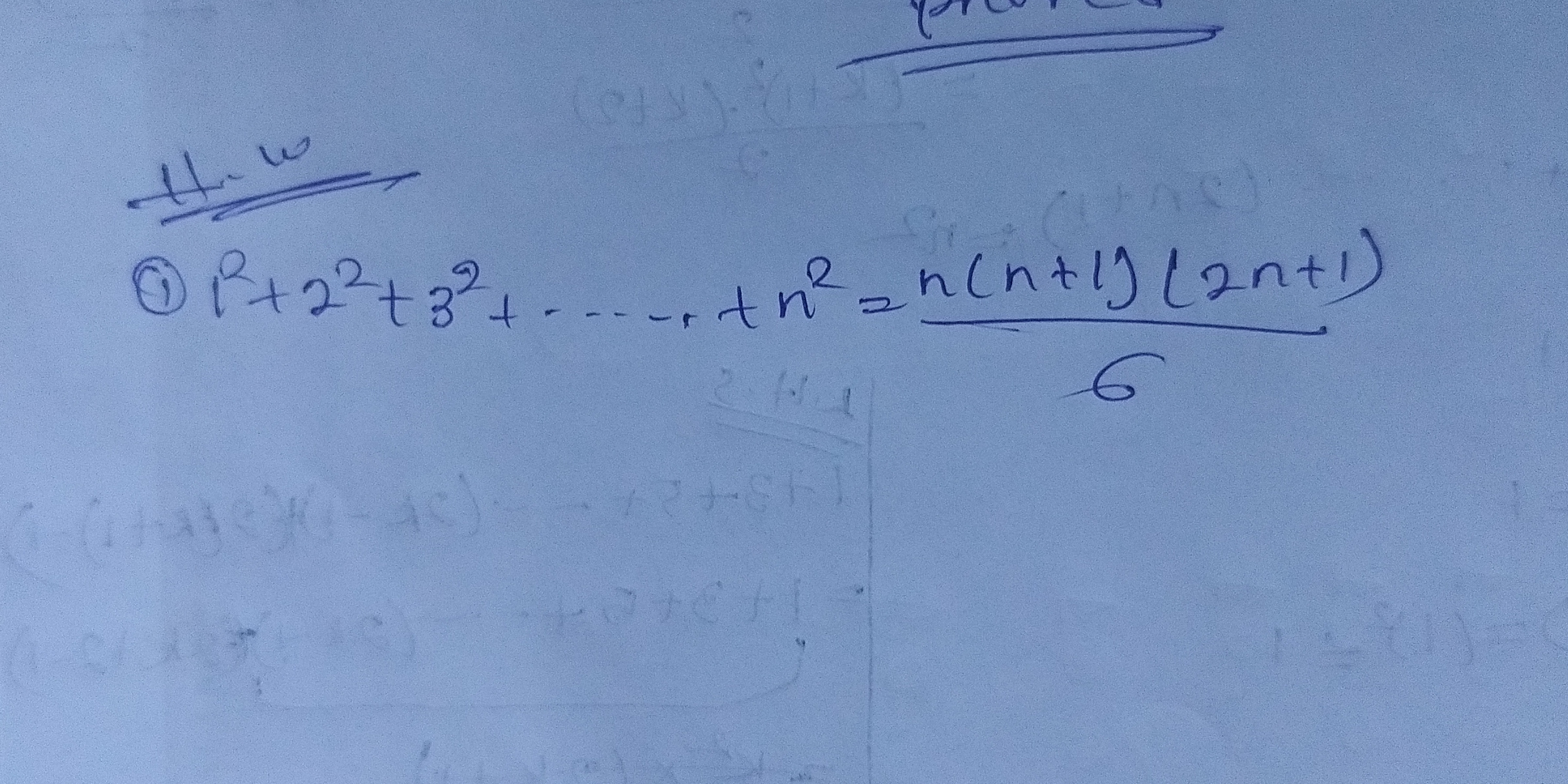
Understand the Problem

The question involves summing a series of squares from 1 to n. It appears to ask for the formula or method to calculate the sum of squares using the provided equation.

Answer

For the sum of squares from 1 to $ n $, use the formula $ S = \frac{n(n+1)(2n+1)}{6} $; for $ n = 5 $, the sum is $ 55 $.

Steps to Solve

Understanding the Sum of Squares Formula

The sum of the squares of the first ( n ) natural numbers is given by the formula:

$$ S = 1^2 + 2^2 + 3^2 + \ldots + n^2 = \frac{n(n+1)(2n+1)}{6} $$

Breaking Down the Formula

This formula can be derived or proven by various methods, but for practical calculations, we simply apply it. First, identify ( n ), which represents how many squares you want to sum.

Calculating the Sum for a Given ( n )

For example, if you want to find the sum of squares from 1 to 5:

Here ( n = 5 ).

Substituting ( n ) into the formula:

$$ S = \frac{5(5+1)(2 \cdot 5 + 1)}{6} $$

Simplifying the Calculation

Now calculate step by step:

( 5 + 1 = 6 )
( 2 \cdot 5 + 1 = 11 )

So,

$$ S = \frac{5 \cdot 6 \cdot 11}{6} $$

Final Calculation

Now multiply the numbers:

( 5 \cdot 6 = 30 )
( 30 \cdot 11 = 330 )

And finally divide by 6:

$$ S = \frac{330}{6} = 55 $$

So, the sum of the squares from 1 to 5 is 55.

The sum of the squares from 1 to ( n ) is given by:

$$ S = \frac{n(n+1)(2n+1)}{6} $$

For ( n = 5 ), the result is ( 55 ).

More Information

The formula for the sum of squares is widely used in statistics, physics, and various fields of mathematics. It helps in calculating variances and dealing with polynomial identities.

Tips

Confusing the sum of squares with the sum of integers: Make sure to apply the correct formula.
As forgetting to use ( n(n + 1)(2n + 1)/6 ) and using a wrong formula can lead to wrong results.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!