100000n + 50n^2 = 93800
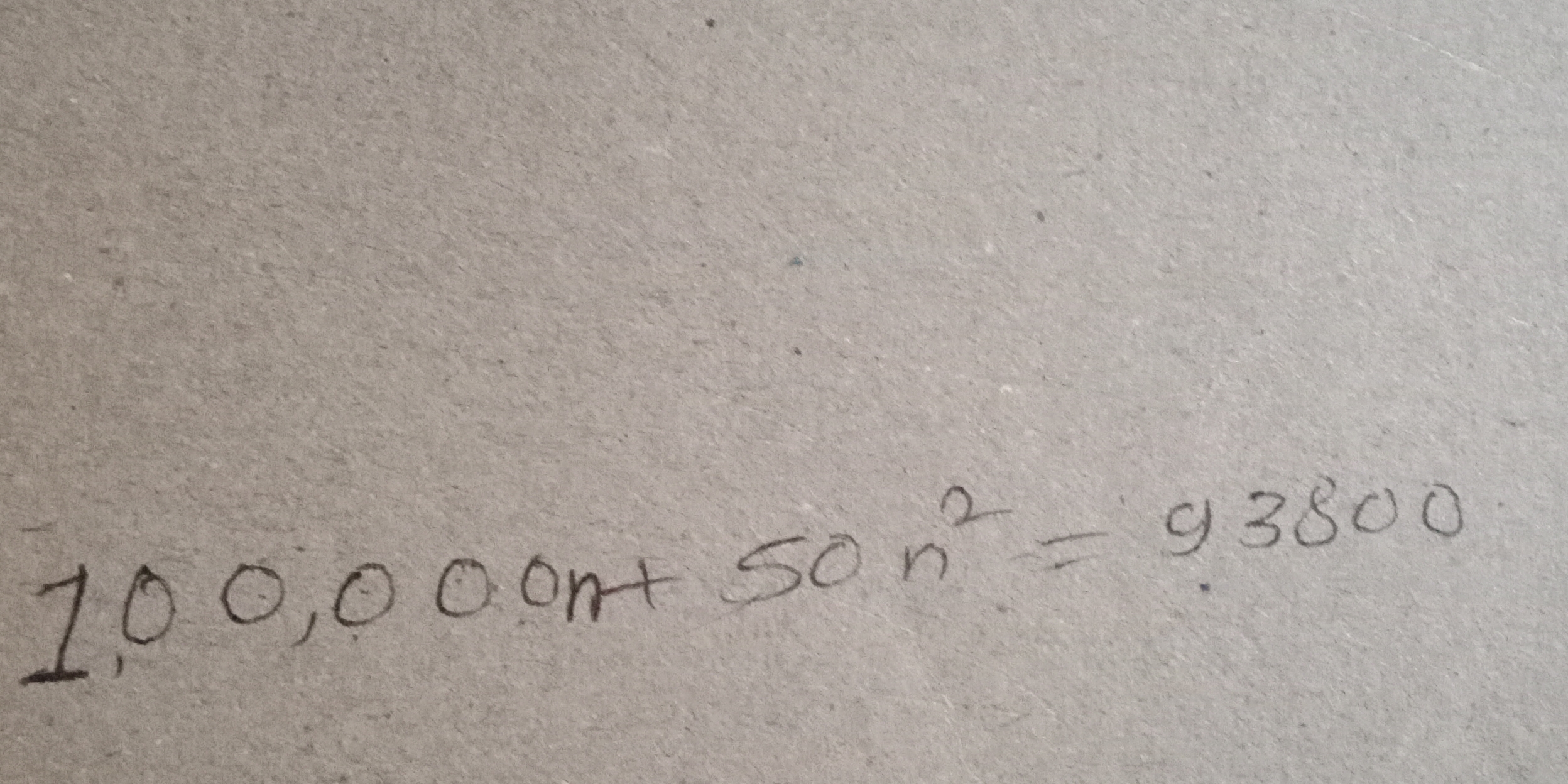
Understand the Problem
The question is an equation in terms of n. It consists of a polynomial equation that sums up to a specific value, suggesting the need to solve for n.
Answer
The value of \( n \) is approximately $0.09$.
Answer for screen readers
The value of ( n ) is approximately $0.09$.
Steps to Solve
- Rearranging the Equation
First, let's rewrite the equation to move all terms to one side: $$ 50n^2 + 100000n - 93800 = 0 $$
- Identifying Coefficients
Here, we identify the coefficients for the quadratic formula:
- ( a = 50 )
- ( b = 100000 )
- ( c = -93800 )
- Applying the Quadratic Formula
Next, we use the quadratic formula: $$ n = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$
- Calculating the Discriminant
Calculate the discriminant, ( b^2 - 4ac ): $$ b^2 = (100000)^2 = 10000000000 $$ $$ 4ac = 4 \cdot 50 \cdot (-93800) = -18760000 $$ $$ \text{Discriminant} = 10000000000 + 18760000 = 10001876000 $$
- Finding the Roots
Now substitute the discriminant back into the quadratic formula: $$ n = \frac{-100000 \pm \sqrt{10001876000}}{2 \cdot 50} $$
- Calculating the Square Root
Calculate the square root: $$ \sqrt{10001876000} \approx 100009 $$
- Calculating the Two Possible Values for n
Now substitute this value back into our equation: $$ n_1 = \frac{-100000 + 100009}{100} = 0.09 $$ $$ n_2 = \frac{-100000 - 100009}{100} = -2000.09 $$
Since ( n ) must be a non-negative value, we take: $$ n \approx 0.09 $$
The value of ( n ) is approximately $0.09$.
More Information
This solution comes from solving a quadratic equation, which is a fundamental skill in algebra. Quadratic equations can represent various real-world scenarios, from physics to finance.
Tips
- Not rearranging the equation correctly: Always ensure the equation is set to zero.
- Errors in the quadratic formula application: Double-check each coefficient and the calculations involving the discriminant.
AI-generated content may contain errors. Please verify critical information