1. Vectors (a) A - B + C (b) A + B - C (c) C - A - B. Given the magnitudes and angles of vectors A, B, and C, perform the calculations.
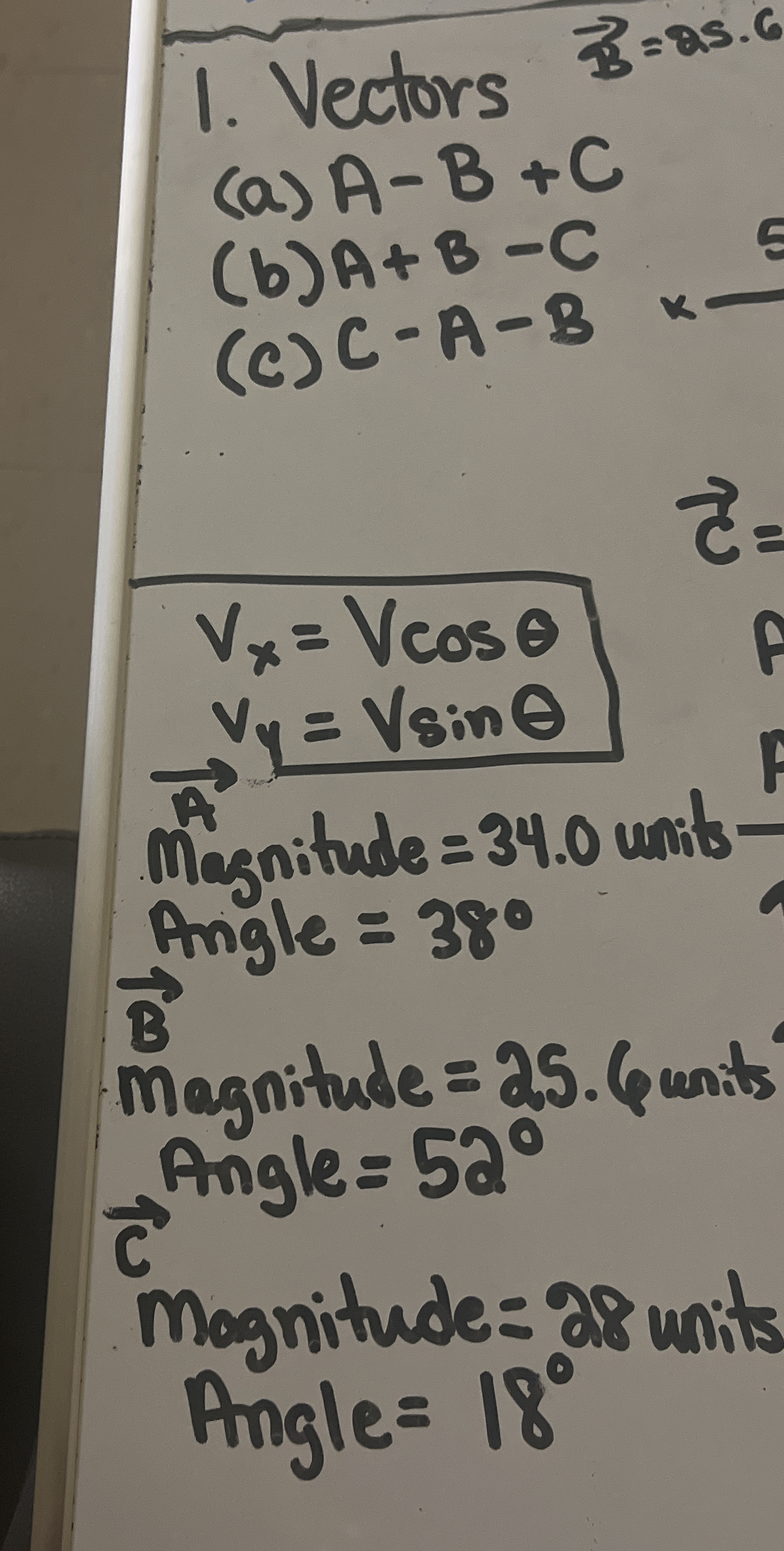
Understand the Problem
The question involves vector operations, specifically calculating vector sums and differences using given magnitudes and angles. It outlines tasks to perform vector additions and subtractions while considering trigonometric calculations for the components of the vectors.
Answer
The resultant vector magnitudes can be calculated using $R = \sqrt{R_x^2 + R_y^2}$ for each operation; angles with $\theta = \tan^{-1}\left(\frac{R_y}{R_x}\right)$.
Answer for screen readers
(a) Magnitude: $R = \sqrt{R_x^2 + R_y^2}$
(b) Magnitude: $R = \sqrt{R_x^2 + R_y^2}$
(c) Magnitude: $R = \sqrt{R_x^2 + R_y^2}$
(Note: Specific numeric results depend on performing the calculations above.)
Steps to Solve
- Calculate Components of Each Vector
We need to calculate the x and y components for each vector using the formulas provided:
For vector A:
- Magnitude = 34.0 units, Angle = 38°
- $$ A_x = 34.0 \cos(38°) $$
- $$ A_y = 34.0 \sin(38°) $$
For vector B:
- Magnitude = 25.6 units, Angle = 52°
- $$ B_x = 25.6 \cos(52°) $$
- $$ B_y = 25.6 \sin(52°) $$
For vector C:
- Magnitude = 28.0 units, Angle = 18°
- $$ C_x = 28.0 \cos(18°) $$
- $$ C_y = 28.0 \sin(18°) $$
- Perform Vector Calculations for Each Case
Now we'll calculate each vector operation:
(a) For vector operation ( A - B + C ):
- $$ R_x = A_x - B_x + C_x $$
- $$ R_y = A_y - B_y + C_y $$
(b) For vector operation ( A + B - C ):
- $$ R_x = A_x + B_x - C_x $$
- $$ R_y = A_y + B_y - C_y $$
(c) For vector operation ( C - A - B ):
- $$ R_x = C_x - A_x - B_x $$
- $$ R_y = C_y - A_y - B_y $$
- Calculate the Magnitudes of Resultant Vectors
Once we have ( R_x ) and ( R_y ) for each case, we can find the magnitudes of the resultant vectors:
- For each ( R ): $$ R = \sqrt{R_x^2 + R_y^2} $$
- Calculate Angles of Resultant Vectors
The angles can also be calculated using:
- $$ \theta = \tan^{-1}\left(\frac{R_y}{R_x}\right) $$
(a) Magnitude: $R = \sqrt{R_x^2 + R_y^2}$
(b) Magnitude: $R = \sqrt{R_x^2 + R_y^2}$
(c) Magnitude: $R = \sqrt{R_x^2 + R_y^2}$
(Note: Specific numeric results depend on performing the calculations above.)
More Information
Vector operations involve calculating components based on magnitudes and angles, using trigonometric functions. These operations are fundamental in physics for understanding forces, displacement, and other vector quantities.
Tips
- Neglecting signs: Ensure correct signs are applied when subtracting vectors.
- Incorrect angle measures: Make sure angles are in the correct units (degrees vs. radians).
- Forgetting to use trigonometric identities correctly: Double-check calculations for ( \cos ) and ( \sin ).
AI-generated content may contain errors. Please verify critical information