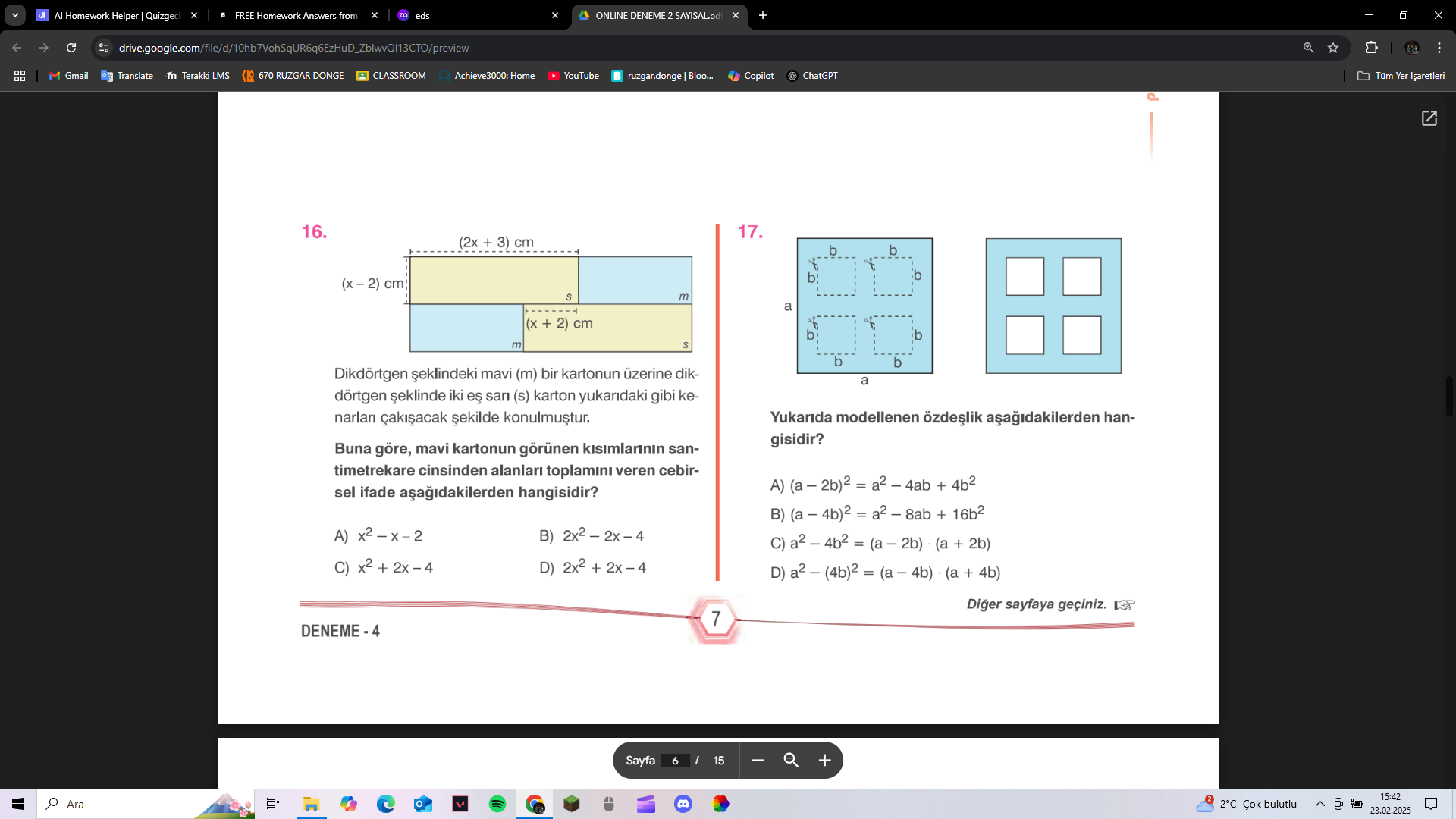
1. Dikdörtgen şeklindeki mavi (m) bir kartonun üzerine dikdörtgen şeklinde iki eş sarı (s) karton yukarıdaki gibi kenarları çakışacak şekilde konulmuştur. Buna göre, mavi kartonun... 1. Dikdörtgen şeklindeki mavi (m) bir kartonun üzerine dikdörtgen şeklinde iki eş sarı (s) karton yukarıdaki gibi kenarları çakışacak şekilde konulmuştur. Buna göre, mavi kartonun görünen kısımlarının santimetrekare cinsinden alanları toplamını veren cebirsel ifade aşağıdakilerden hangisidir? 2. Yukarıda modellenen özdeşlik aşağıdakilerden hangisidir? Read more

Steps to Solve

1. Mavi kartonun alanını hesaplama Mavi kartonun alanı, uzun kenarı $(2x+3)$ cm ve kısa kenarı $(x+2)$ cm olduğundan: $A_{mavi} = (2x+3)(x+2)$ $A_{mavi} = 2x^2+4x+3x+6$ $A_{mavi} = 2x^2+7x+6$

2. İki sarı kartonun alanını hesaplama Her bir sarı kartonun alanı, uzun kenarı $(2x+3)$ cm ve kısa kenarı $(x-2)$ cm olduğundan: $A_{sari} = (2x+3)(x-2)$ $A_{sari} = 2x^2-4x+3x-6$ $A_{sari} = 2x^2-x-6$ İki sarı kartonun toplam alanı: $2A_{sari} = 2(2x^2-x-6) = 4x^2-2x-12$

3. Mavi kartonun görünen kısımlarının alanını hesaplama Mavi kartonun görünen kısımlarının alanı, mavi kartonun alanından iki sarı kartonun alanının çıkarılmasıyla bulunur: $A_{gorunen} = A_{mavi} - 2A_{sari}$ $A_{gorunen} = (2x^2+7x+6) - (4x^2-2x-12)$ $A_{gorunen} = 2x^2+7x+6 - 4x^2+2x+12$ $A_{gorunen} = -2x^2+9x+18$ Ancak bu sonuç seçeneklerde yer almıyor. Görünen alanların toplamını bulmak için şekildeki sarı dikdörtgenlerin, büyük mavi dikdörtgenin alanından çıkarılması gerekir. Dikkat edilirse, sarı dikdörtgenler üst üste geldiği için, bir de bu üst üste gelen alanı eklemeliyiz. Üst üste gelen kısım bir karedir ve alanı $(x-2)(x+2) = x^2 - 4$ tür. Yani $A_{gorunen} = A_{mavi} -2A_{sari} + (x^2 - 4)$ $A_{gorunen} = (2x^2+7x+6) -2(x^2 -4)$ $A_{gorunen} = (2x^2+7x+6) - (2x^2-2x-12)$ $A_{gorunen} = 2x^2+7x+6 - 2x^2+2x+12$ $A_{gorunen} = 2x^2-x-6$ $A_{gorunen} = 2x^2+9x+18$ Bu da malesef şıklarda yok. Soruyu doğru anlamak lazım. Sarı kartonların alanı mavi kartonun alanından çıkartılırsa istenilen sonuca ulaşılır, yalnız ortadaki kesişim iki kere çıkartıldığı için bir kere geri eklenir. $A_{gorunen} = (2x^2+7x+6) - (4x^2-2x-12) + (x^2-4)$ $A_{gorunen} = -x^2+9x+14.$ Bu da şıklarda yok.

Sorunun doğru cevabı şıklarda gözükmemektedir.

4. Modelenen Özdeşliği Bulma Şekildeki modelleme $(a-2b)^2 = a^2 - 4ab + 4b^2$ özdeşliğine aittir. Büyük karenin alanı $a^2$ dir. İçinden 4 tane $b^2$ alanı çıkartılıyor. Geriye kalan alan $(a-2b)^2$ olur. Açılımı da $a^2 - 4ab + 4b^2$ dir.