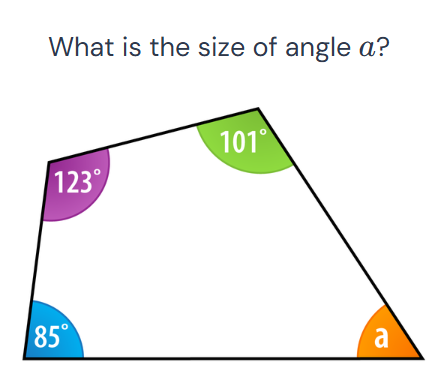
What is the size of angle a in the quadrilateral?
Understand the Problem
The question asks to find the measure of angle 'a' in a quadrilateral, given the measures of the other three angles. To solve this, we need to remember that the sum of the interior angles in a quadrilateral is 360 degrees. Then we can set up an equation to solve for 'a'.
Answer
$a = 51^{\circ}$
Answer for screen readers
$a = 51^{\circ}$
Steps to Solve
- Sum of angles in a quadrilateral
The sum of the interior angles in any quadrilateral is 360 degrees.
- Set up the equation
We can write the equation: $101 + 123 + 85 + a = 360$
- Combine known angles
Add the known angle values: $101 + 123 + 85 = 309$
So, the equation becomes: $309 + a = 360$
- Solve for a
Subtract 309 from both sides of the equation: $a = 360 - 309$ $a = 51$
$a = 51^{\circ}$
More Information
The angle $a$ is 51 degrees, which makes the sum of all angles equal to $360^\circ$, satisfying the property of a quadrilateral.
Tips
A common mistake is to forget that the angles of a quadrilateral add up to 360 degrees. Another mistake would be incorrect arithmetic when summing the known angles or when subtracting from 360.
AI-generated content may contain errors. Please verify critical information