1 + 4 = 5, 2 + 5 = 12, 3 + 6 = 21, 8 + 11 = ?
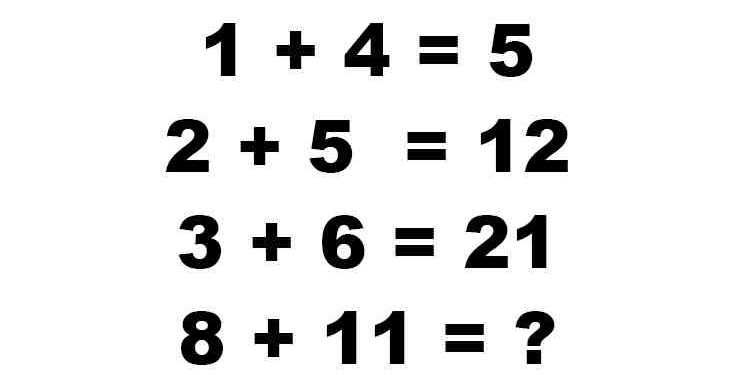
Understand the Problem
The question is presenting a sequence of equations that follow a specific pattern, and it is asking to determine the result of the last equation based on the established pattern.
Answer
The final result of $8 + 11$ is $96$.
Answer for screen readers
The result of the equation $8 + 11$ is $96$.
Steps to Solve
-
Identify the Pattern
Look at the sequences given:
- For $1 + 4$: The result is $5$. This can be thought of as $1 \times 4 + 1$.
- For $2 + 5$: The result is $12$. This can be expressed as $2 \times 5 + 2$.
- For $3 + 6$: The result is $21$. This can be represented as $3 \times 6 + 3$.
-
Formulate the Rule
Based on the examination of the first three equations, the pattern can be described as follows:
$$ a + b = a \times b + a $$
where $a$ and $b$ are the numbers being added.
-
Apply the Pattern to the Last Equation
Now, apply this rule to the last equation $8 + 11$:
$$ 8 + 11 = 8 \times 11 + 8 $$
-
Calculate the Result
Now perform the multiplication and addition:
- Calculate $8 \times 11 = 88$.
- Then add $8$:
$$ 88 + 8 = 96 $$
The result of the equation $8 + 11$ is $96$.
More Information
This problem illustrates a creative way to look at a sequence of equations that do not follow standard arithmetic rules. Instead, they use a pattern-based approach.
Tips
- Overlooking the pattern: It's easy to assume standard addition is being used without looking for an underlying rule. Always explore different approaches to find the correct pattern.
- Miscalculating: Ensure careful arithmetic, especially when multiplying and adding large numbers.
AI-generated content may contain errors. Please verify critical information