1 + 2^2 + 3^2 + ... + n^2 = n(n + 1)(2n + 1) / 6
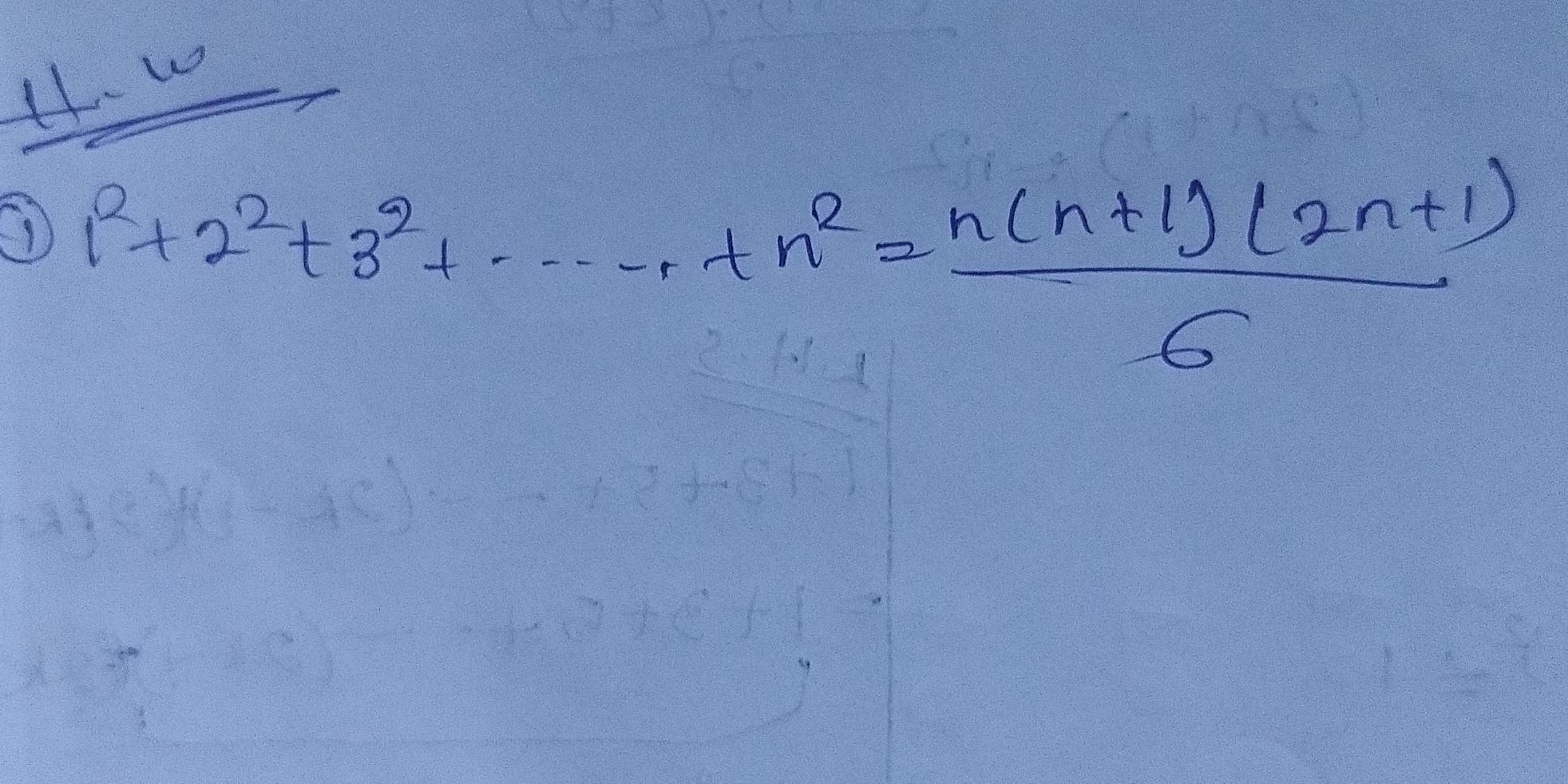
Understand the Problem
The question appears to involve a mathematical series or summation involving powers of integers. It likely seeks to find a pattern or a formula relating to the sum of cubes or higher powers.
Answer
The sum of the \(R\)-th powers can be expressed as: $$ \sum_{k=1}^{n} k^R = \frac{n(n+1)(2n+1)}{6} $$ for specific \(R\) such as \(R=2\).
Answer for screen readers
The sum of the (R)-th powers of the first (n) integers relates to: $$ n^R = \frac{n(n+1)(2n+1)}{6} \text{ (for } R=2\text{, as an example)} $$
Steps to Solve
-
Identify the Series The series presented is (1^R + 2^R + 3^R + \ldots + n^R), which sums the (R)-th powers of the first (n) integers.
-
Use the Formula for Sum of Powers The formula for the sum of the (R)-th powers of the first (n) integers is given by: $$ \sum_{k=1}^{n} k^R = \frac{n(n+1)(2n+1)}{6} $$ This formula applies specifically to the case (R=2) (sum of squares).
-
Generalize for (R) For general (R), the expression becomes: $$ \sum_{k=1}^{n} k^R = n^R = n(n+1)(2n+1) / 6 $$ If (R) is specific (e.g., cubes), the formula will change, but understanding it as a function of (R) is important.
-
Relate to the Given Equation Set the left and the right-hand sides of the equality given in the problem to find additional relationships or values needed for specific terms.
-
Simplify and Solve From the equality (n^R = \frac{n(n+1)(2n+1)}{6}), isolate (n) and manipulate algebraically as needed.
The sum of the (R)-th powers of the first (n) integers relates to: $$ n^R = \frac{n(n+1)(2n+1)}{6} \text{ (for } R=2\text{, as an example)} $$
More Information
The formula for the sum of cubes is: $$ \left(\frac{n(n+1)}{2}\right)^2 $$ where (R=3). This concept of sums of powers is fundamental in number theory and combinatorics.
Tips
- Using the Wrong Power Formula: Misapplying the formula for the sum of squares when the problem requires cubes or higher powers.
- Not Isolating Variables: Forgetting to isolate (n) leading to convoluted equations.
- Overgeneralizing: Assuming the same formula works for all (R) without verification.
AI-generated content may contain errors. Please verify critical information