(1 1) · (x1) = (3) (2 2) (x2) (7)
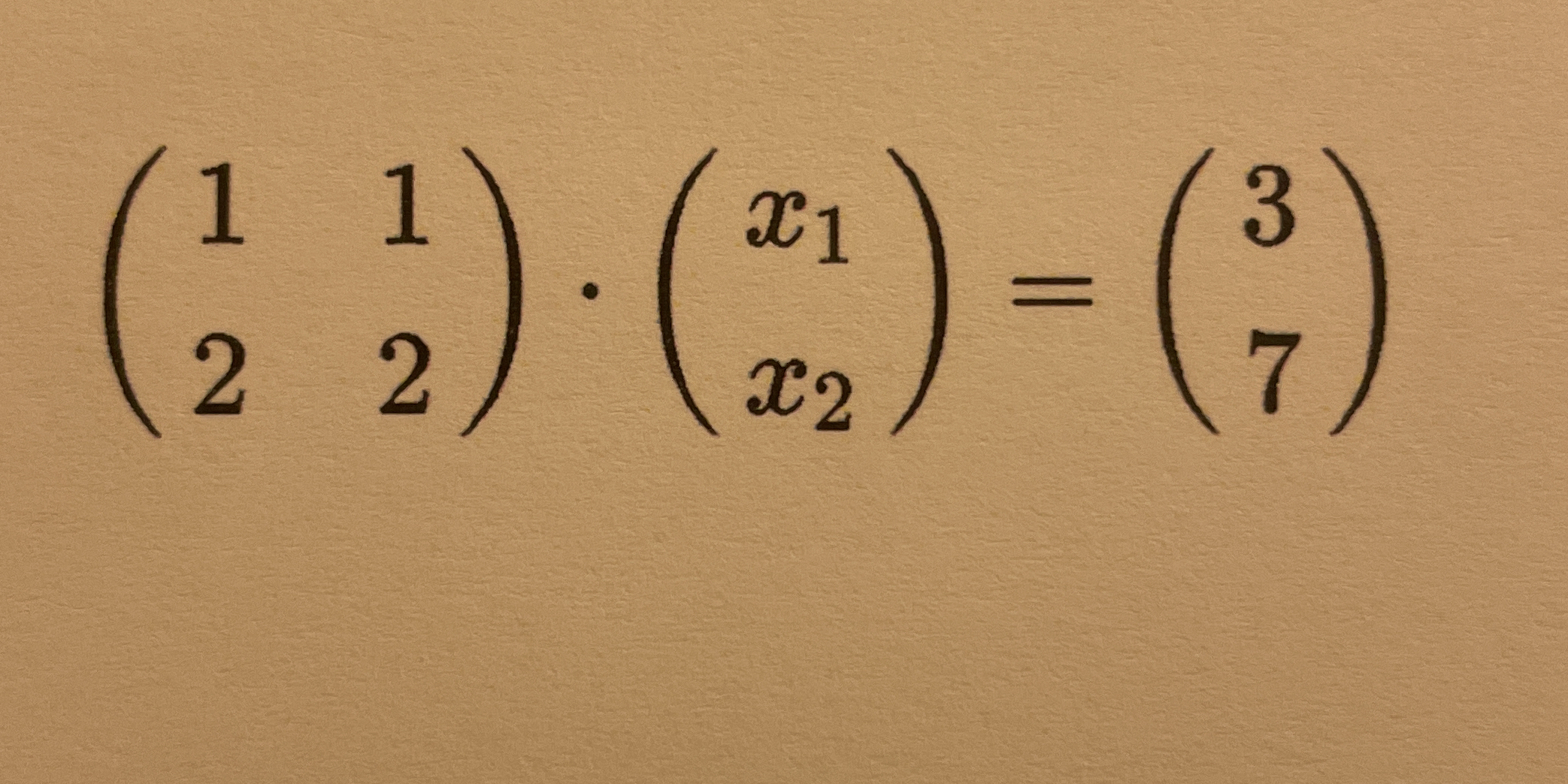
Understand the Problem
The question involves solving a system of linear equations represented in matrix form. The goal is to find the values of x1 and x2 that satisfy the equation.
Answer
No unique solution exists.
Answer for screen readers
No unique solution exists for the system of equations.
Steps to Solve
-
Set up the equations
From the matrix equation, we can derive two linear equations: [ 1 \cdot x_1 + 1 \cdot x_2 = 3 \quad \text{(Equation 1)} ] [ 2 \cdot x_1 + 2 \cdot x_2 = 7 \quad \text{(Equation 2)} ]
-
Simplify Equation 2
Divide the entire second equation by 2 for simplicity: [ x_1 + x_2 = \frac{7}{2} \quad \text{(Simplified Equation 2)} ]
-
Substitute values from Equation 1 into Simplified Equation 2
From Equation 1, we can express ( x_2 ): [ x_2 = 3 - x_1 ] Substitute this into the Simplified Equation 2: [ x_1 + (3 - x_1) = \frac{7}{2} ]
-
Solve for ( x_1 )
Simplifying gives: [ 3 = \frac{7}{2} ] This is not valid, indicating the equations are dependent.
-
Verify Dependency
Since multiplying the first equation by 2 gives: [ 2x_1 + 2x_2 = 6 ] and we already have ( 2x_1 + 2x_2 = 7 ). The system has no unique solution; it is inconsistent.
No unique solution exists for the system of equations.
More Information
The equations are dependent because they represent parallel lines, which do not intersect. This indicates there is no point that satisfies both equations simultaneously.
Tips
- Assuming there is always a solution without checking for consistency.
- Forgetting to simplify and check for equivalent equations.
AI-generated content may contain errors. Please verify critical information