(1 1) · (x1) = (3) (2 2) (x2) (6)
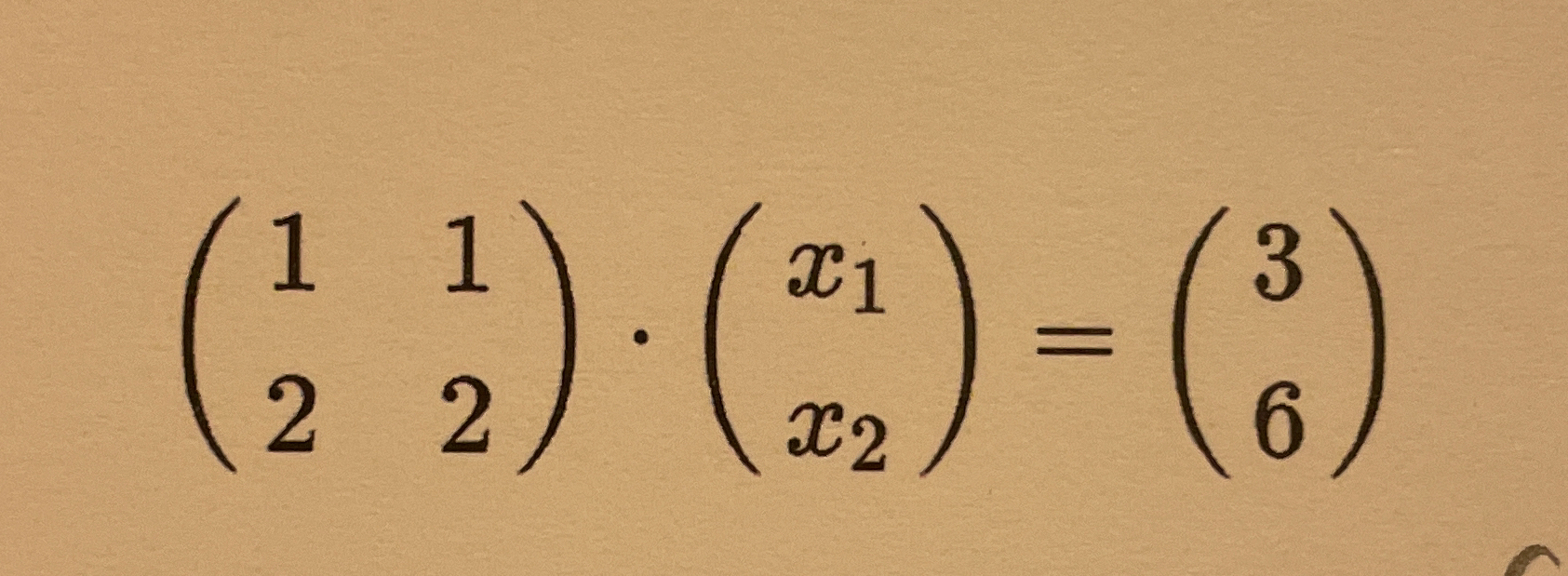
Understand the Problem
The question involves a matrix multiplication equation, where a 2x2 matrix is multiplied by a column vector, resulting in another column vector. The goal is to find the values of x1 and x2 that satisfy the equation.
Answer
The solutions are $ (x_1, x_2) = (3, 0) $ or any other pairs satisfying $ x_1 + x_2 = 3 $.
Answer for screen readers
The solutions for the system of equations are $(x_1, x_2) = (3, 0)$, but there are infinitely many solutions such as $(x_1, x_2) = (2, 1)$, $(1, 2)$, etc.
Steps to Solve
- Set up the equation from the matrix multiplication
The equation can be set up based on the matrix multiplication of the 2x2 matrix and the column vector:
$$ \begin{pmatrix} 1 & 1 \ 2 & 2 \end{pmatrix} \begin{pmatrix} x_1 \ x_2 \end{pmatrix}
\begin{pmatrix} 3 \ 6 \end{pmatrix} $$
- Write the equations based on the multiplication
The multiplication leads to two equations:
From the first row: $$ 1 \cdot x_1 + 1 \cdot x_2 = 3 $$ From the second row: $$ 2 \cdot x_1 + 2 \cdot x_2 = 6 $$
- Simplify the second equation
Divide the entire second equation by 2 to simplify it:
$$ x_1 + x_2 = 3 $$
- Solve the system of equations
Now we have:
- From the first equation: $x_1 + x_2 = 3$
- From the simplified second equation: $x_1 + x_2 = 3$
Both equations are the same; thus, we can express one variable in terms of the other.
Let’s solve for $x_1$:
$$ x_1 = 3 - x_2 $$
- Choose a value for $x_2$
Choose any value for $x_2$. For example, if we let $x_2 = 0$, then: $$ x_1 = 3 - 0 = 3 $$
Thus one solution is $(x_1, x_2) = (3, 0)$. You could choose any value for $x_2$ to find other solutions.
The solutions for the system of equations are $(x_1, x_2) = (3, 0)$, but there are infinitely many solutions such as $(x_1, x_2) = (2, 1)$, $(1, 2)$, etc.
More Information
This represents a case of dependent equations, where there are infinitely many solutions along the line described by the equation $x_1 + x_2 = 3$.
Tips
- Not recognizing that the second equation simplifies to the first, leading to the conclusion that there are infinitely many solutions.
- Failing to choose a specific $x_2$ value when expressing $x_1$ in terms of $x_2$.
AI-generated content may contain errors. Please verify critical information