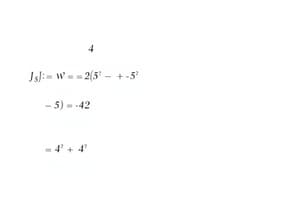Podcast
Questions and Answers
What is the primarily purpose of a flowchart?
What is the primarily purpose of a flowchart?
- To communicate the logic of a program and making it easy to understand (correct)
- To directly modify program logic
- To write the full computer program
- To act as a source document for final distribution to users
In a flowchart, the diamond shape represents a process or internal operation.
In a flowchart, the diamond shape represents a process or internal operation.
False (B)
What are the four basic steps involved in finding a solution to a problem?
What are the four basic steps involved in finding a solution to a problem?
Define the problem, generate alternative solutions, evaluate and select an alternative, and implement and follow up on the solution.
A(n) _________ is a set of instructions/steps/rules that are followed to solve a problem.
A(n) _________ is a set of instructions/steps/rules that are followed to solve a problem.
Match the following flowchart symbols with their corresponding function:
Match the following flowchart symbols with their corresponding function:
Which of the following is a key advantage of using an algorithm for problem-solving?
Which of the following is a key advantage of using an algorithm for problem-solving?
In an undirected graph, edges have a defined direction indicating the traversal is only possible in one way.
In an undirected graph, edges have a defined direction indicating the traversal is only possible in one way.
What are the operations that can be performed on an array?
What are the operations that can be performed on an array?
Data elements in a linear data structure are arranged in _________ order, where each element is connected to its previous and next element.
Data elements in a linear data structure are arranged in _________ order, where each element is connected to its previous and next element.
Which of the following data structure follows the LIFO (Last In First Out) principle?
Which of the following data structure follows the LIFO (Last In First Out) principle?
Flashcards
Flowchart
Flowchart
A diagram using different shapes to show the flow of data through a system.
Algorithm vs Flowchart
Algorithm vs Flowchart
Algorithm uses step by step to solve a problem and flowchart is a diagram which shows flow of data through processing system.
Linear Data Structure
Linear Data Structure
A linear data structure with elements in sequential order, linked to the previous element.
Stack
Stack
Signup and view all the flashcards
Push(Stack)
Push(Stack)
Signup and view all the flashcards
Pop(Stack)
Pop(Stack)
Signup and view all the flashcards
Queue
Queue
Signup and view all the flashcards
Enqueue
Enqueue
Signup and view all the flashcards
Dequeue
Dequeue
Signup and view all the flashcards
Decision/Condition(Flowchart)
Decision/Condition(Flowchart)
Signup and view all the flashcards
Study Notes
Funciones vectoriales de variable real
- A function assigns a vector to each real number in a set.
- Vectorial function: $\overrightarrow{r}: I \subseteq \mathbb{R} \longrightarrow \mathbb{R}^n$
- Each real number $t \in I$ is assigned a vector $\overrightarrow{r}(t) = (f_1(t), f_2(t),..., f_n(t))$.
- $f_i: I \subseteq \mathbb{R} \longrightarrow \mathbb{R}$ are real-valued functions.
- Example: $\overrightarrow{r}(t) = (t^2 + 1, \cos(t), e^t)$ is a function with $n = 3$.
Límite
- The limit of a vector function $\overrightarrow{r}(t)$ as $t$ approaches $t_0$ is given by:
- $\lim_{t \to t_0} \overrightarrow{r}(t) = (\lim_{t \to t_0} f_1(t), \lim_{t \to t_0} f_2(t),..., \lim_{t \to t_0} f_n(t))$ if all component limits exist.
Continuidad
- A vector function $\overrightarrow{r}(t)$ is continuous at $t_0$ under three conditions:
- $\overrightarrow{r}(t_0)$ exists.
- $\lim_{t \to t_0} \overrightarrow{r}(t)$ exists.
- $\lim_{t \to t_0} \overrightarrow{r}(t) = \overrightarrow{r}(t_0)$
- $\overrightarrow{r}(t)$ is continuous at $t_0$ if each component function $f_i(t)$ is continuous at $t_0$.
Derivada
- The derivative of a vector function $\overrightarrow{r}(t)$ is:
- $\overrightarrow{r}'(t) = \lim_{h \to 0} \frac{\overrightarrow{r}(t+h) - \overrightarrow{r}(t)}{h} = (f_1'(t), f_2'(t),..., f_n'(t))$
- This is only if all component function derivatives exist.
- Notation: $\overrightarrow{r}'(t) = \frac{d\overrightarrow{r}}{dt}$
- Geometrically, if $\overrightarrow{r}(t)$ is a particle's position at time $t$, $\overrightarrow{r}'(t)$ is its velocity vector.
- $\overrightarrow{r}'(t)$ is tangent to the path of $\overrightarrow{r}(t)$ at point $\overrightarrow{r}(t)$.
Reglas de derivación
- Given differentiable vector functions $\overrightarrow{r}(t)$ and $\overrightarrow{s}(t)$, and a differentiable scalar function $f(t)$:
- $(\overrightarrow{r}(t) + \overrightarrow{s}(t))' = \overrightarrow{r}'(t) + \overrightarrow{s}'(t)$
- $(c\overrightarrow{r}(t))' = c\overrightarrow{r}'(t)$, where $c$ is a constant.
- $(f(t)\overrightarrow{r}(t))' = f'(t)\overrightarrow{r}(t) + f(t)\overrightarrow{r}'(t)$
- $(\overrightarrow{r}(t) \cdot \overrightarrow{s}(t))' = \overrightarrow{r}'(t) \cdot \overrightarrow{s}(t) + \overrightarrow{r}(t) \cdot \overrightarrow{s}'(t)$
- $(\overrightarrow{r}(t) \times \overrightarrow{s}(t))' = \overrightarrow{r}'(t) \times \overrightarrow{s}(t) + \overrightarrow{r}(t) \times \overrightarrow{s}'(t)$
- $(\overrightarrow{r}(f(t)))' = \overrightarrow{r}'(f(t)) \cdot f'(t)$ (Chain Rule)
Transductores y sensores
- Transducers convert one form of energy into another.
- Sensors are transducers that measure physical quantities and convert them into electrical signals.
Clasificación de los transductores
- Based on Energy Conversion:
- Resistive: Converts resistance changes to electrical signals. –Capacitive: Converts capacitance changes to electrical signals.
- Inductive: Converts inductance changes to electrical signals.
- Piezoelectric: Converts pressure to electrical signals.
- Thermoelectric: Converts temperature changes to electrical signals.
- Based on Output Signal:
- Analog: Continuous output proportional to measured quantity.
- Digital: Discrete output representing measured quantity.
- Based on Measured Quantity:
- Temperature, Pressure, Flow, Level, Position, Velocity, Acceleration.
Características de los transductores
- Sensitivity is the ratio of output signal change to the physical quantity change.
- $S = \frac{\Delta V_o}{\Delta p}$
- Resolution is the smallest detectable change.
- Precision is the difference between measured and actual values.
- Accuracy is the ability to produce a measurement close to the true value.
- Linearity measures output signal proportionality to measured quantity.
- Range: the interval of measurable values
- Response Time is the time for the signal to reach a stable value.
- Hysteresis is the difference between increasing and decreasing signal.
Aplicaciones de los transductores
- Applications include industrial automation, medicine, automotive systems, and consumer electronics.
- Automated systems employ transducers to control and monitor industrial processes.
- Measure vital signs, such as temperature, blood pressure and heart rate
- Automotive industry uses them to control and monitor engine performance, tire pressure, and vehicle speed.
Transductores resistivos
- Resistive transducers measure physical quantities based on resistance change.
Potenciómetros
- Potentiometers measure linear or angular position.
- Fixed resistor with sliding contact.
- Output voltage is proportional to contact position.
- Equation: $V_o = V_i \cdot \frac{R_2}{R_1 + R_2}$
- Limited by number of wire turns or size of resistive material grains.
- Used for volume control, position sensing, and voltage adjustment.
Galgas extensométricas
- Strain gauges measure object deformation.
- Thin resistive material sheet attached to the object.
- Resistance change occurs during deformation
- Equation: $R = \rho \frac{L}{A}$, where R is resistance, $\rho$ is resistivity, L is length, and A is cross-sectional area.
- Gauge Factor (GF): $GF = \frac{\Delta R / R}{\epsilon}$, where $\epsilon$ is strain.
- Strain gauges mounted on a Wheatstone bridge
- Temperature compensation needed for accurate strain measurements.
- Used for deformation measurement, force measurement in scales, and pressure measurement in pressure sensors.
Termistores
- Thermistors are temperature-sensitive resistors.
- NTC (Negative Temperature Coefficient) thermistors decrease resistance with increasing temperature.
- PTC (Positive Temperature Coefficient) thermistors increase resistance with temperature.
- Steinhart-Hart Equation models resistance-temperature relationship for NTCs: $\frac{1}{T} = A + B \ln(R) + C (\ln(R))^3$
- Linearization circuits improve measurement accuracy.
- Used in thermostats, temperature control systems, and liquid/gas flow measurement.
RTD
- RTD (Resistance Temperature Detector) measures temperature via metal resistance change.
- Common materials are platinum (Pt), nickel (Ni), and copper (Cu).
- Equation: $R_T = R_0 [1 + \alpha (T - T_0)]$, where $R_T$ is resistance at temperature T.
- Different configurations include two-wire, three-wire, and four-wire RTDs.
- RTDs offer high accuracy and reasonable linearity.
- More expensive compared to thermistors and require current that causes self-heating
- Used in industrial processes, lab equipment, and HVAC systems.
Transductores capacitivos
- Capacitive transducers measure physical quantities based on capacitance change.
- Change in capacitance is used to measure the physical quantity
- Capacitance is proportional to plate area and inversely proportional to plate distance.
- $C = \epsilon \frac{A}{d}$, where C is capacitance, $\epsilon$ is permittivity, A is area, and d is distance.
- Vary capacitance by changing plate area, separation, or dielectric permittivity.
- High sensitivity, low output impedance, and low power consumption
- Sensitivity to temperature, humidity, and vibrations
Transductores inductivos
- Inductive transducers measure physical quantities based on inductance change.
- Types:
- LVDT: Measures linear displacement using a moving core.
- Resolvers/Syncros: Measure angular position via a rotor and stator.
- LVDT Advantages
- High precision
- High resolution
- Low output impedance
- The ability to measure large quantities
- LVDT Disadvantages
- Sensitive to temperature
- Sensitive to humidity
- No linearity
- Applications:
- Position
- Speed -Acceleration
Transductores piezoeléctricos
- Piezoelectric transducers measure physical quantities using the piezoelectric effect.
- Materials generate electric charge when pressure is applied.
- Materials include natural crystals, polarized ceramics, and polymers
- High sensitivity and frequency response
- Sensitivity to temperature, humidity, and vibrations
- Require a charge amplifier and is susceptible to non-liniarity
- Used for pressure, force, and acceleration measurement.
Transductores termoeléctricos
- Thermoelectric transducers measure temperature using the Seebeck effect.
- A voltage is generated when two different metals at the junctions are at different temperatures.
- Types: J, K, T, E, N, S, R, B
- Offers a wide range and is both simple and robust
- Characterized by low sensitivity and requirement for cold junction compensation
- Used in furnaces, engines, chemical processes, and HVAC systems.
Mobile App User Guide
- Introduces mobile app guide for understanding app features.
Getting Started
- App is downloadable from Apple App Store or Google Play Store.
- Installation steps involve opening the app store, searching for the app, and opening it. Creating an Account: steps include pressing on "Create account", entering relevant details, and verifying the email address.
- Logging In Steps: opening the app, inserting credentials and pressing on "Log In"
Navigating the App
- Offers quick access to main features like Home, Search, Add, Notifications, and Profile.
- Provides access to Settings, Help, Contact, and Log Out.
Features
- Characteristic 1: [Feature 1 description]. Use: [Step 1], [Step 2], [Step 3].
- Characteristic 2: [Feature 2 description]. Use: [Step 1], [Step 2], [Step 3].
- Characteristic 3: [Feature 3 description]. Use: [Step 1], [Step 2], [Step 3].
Settings
- Customizing the User Profile, configure notification preferences, and adjust privacy settings from account panel.
Troubleshooting
- Providing some standard solutions to problems the end-user my face.
- Problems and solutions described.
FAQ
- Frequently answered question.
- Answered questions listed.
Contact
- Provided contact us details for questions or more help .
Chapter 14: Social Psychology
- Social psychology studies how people affect each other's thoughts, feelings, and behaviors.
- The field studies both the self and the social world.
Areas of Social Psychology
- Intrapersonal processes include emotions, attitudes, self-concept, and social cognition.
- Interpersonal processes include helping behavior, aggression, prejudice and discrimination, attraction, and relationships.
Attitudes and Persuasion
What is an Attitude?
- An attitude includes affective, behavioral, and cognitive components.
- Feelings, behavior, belief, and knowledge
How Attitudes Change
- Persuasion changes an attitude toward something based on communications.
Yale Attitude Change Approach
- States that certain sources, such as credibility and attractiveness, are key to persuasiveness.
- Elements of the message, such as subtlety or timing, influence persuasiveness
- Audience attention, intelligence, self-esteem, and age
Elaboration Likelihood Model
- Model of persuasion.
- It has two routes: Central route: logic-driven, using facts. Peripheral route: less direct and relies on emotion or celebrity endorsement to associate positivity.
Tension
What is Tension?
- Is pulling force from opposite ends.
- Opposite of compression.
Tension formula
- Formula: $T = (m \times g) + (m \times a)$
- Where:
- $T =$ Tension (N)
- $m =$ mass (kg)
- $g =$ acceleration due to gravity (9.8 m/s²)
- $a =$ acceleration of the object (m/s²)
- Example
- A 5kg mass is hanging from a ceiling using a string. Calculate the tension in the string.
- Therefore, the tension in the string is 49N.
Lecture 10
The Pendulum
Simple Pendulum
- Idealizations
- Mass concentrated at point
- Massless string
- No air resistance
- No friction at the hinge
- $\theta$ The angular displacement
- s is the arc length
- $s = L\theta$
- $\theta = s/L$
- Restoring force:
- $F_t = -mgsin\theta$
- $ma = -mgsin\theta$
- $a = -gsin\theta$
- For small angles:
- $sin\theta \approx \theta$
- $a = -g\theta = -g\frac{s}{L}$
- $a = -\frac{g}{L}s$
- $\omega^2 = \frac{g}{L}$
- $\omega = \sqrt{\frac{g}{L}}$
- $T = \frac{2\pi}{\omega} = 2\pi\sqrt{\frac{L}{g}}$
Physical Pendulum
- Not all mass concentrated at one point.
- Extended object of mass M.
D is the distance from the pivot to the center of mass.
- $\tau = -MgDsin\theta = I\alpha$
- $\alpha = \frac{\tau}{I} = -\frac{MgD}{I}sin\theta$
- $\alpha \approx -\frac{MgD}{I}\theta$
- $\omega = \sqrt{\frac{MgD}{I}}$
- $T = 2\pi\sqrt{\frac{I}{MgD}}$
- If $I = MD^2$
- $T = 2\pi\sqrt{\frac{MD^2}{MgD}} = 2\pi\sqrt{\frac{D}{g}}$
Example
- A meter stick is pivoted at one end
- $I = \frac{1}{3}ML^2$ D = $\frac{L}{2}$
- $T = 2\pi\sqrt{\frac{\frac{1}{3}ML^2}{Mg\frac{L}{2}}} = 2\pi\sqrt{\frac{2L}{3g}} = 2\pi\sqrt{\frac{2(1m)}{3(9.8m/s^2)}} = 1.64s$
Damped Oscillations
- $F_{damping} = -bv$
- $F = ma = -kx - bv$
- $ma + bv + kx = 0$
- $x(t) = Ae^{-\frac{b}{2m}t}cos(\omega't + \phi)$
- $\omega' = \sqrt{\frac{k}{m} - (\frac{b}{2m})^2}$
Types of Damping
- Underdamped: Light damping, oscillates with decreasing amplitude.
- Critically damped: Returns to equilibrium as quickly as possible without oscillating
- Overdamped: Returns to equilibrium slowly without oscillating
Forced Oscillations and Resonance
- Driving force $F(t) = F_0sin(\omega t)$
- $A = \frac{F_0/m}{\sqrt{(\omega^2 - \omega_0^2)^2 + (b\omega/m)^2}}$
- $\omega_0 = \sqrt{\frac{k}{m}}$
- Resonance when $\omega = \omega_0$
- If damping is small, the amplitude is large
The Mathematics of Data Science
Course Overview
- Code: Ma 305
- Instructor: Prof Broderick
- Credits: 3
- Level: Intermediate
- Term: Fall 2023-2024
- Prerequisites: Ma 121 and proficiency in Python
Course Description
- Focuses on mathematical concepts essential for data science.
- Application of Concepts with Python.
Learning Objectives
- Apply calculus techniques and linear algebra to solve data science problems.
- Use Python for data analysis and visualization.
Course Schedule
- Introduction to Data Science Mathematics.
- Linear Algebra: Vectors and Matrices, Linear Transformations.
- Calculus: Differentiation, Optimization: Gradient Descent.
- Probability Theory: Random Variables and Statistical Inference.
- Regularization Ridge, Lasso and Elastic Net.
- Midterm Exam Covers topics from weeks 1-8.
- Clustering and Dimensionality Reduction: PCA.
Recommender Systems and Time Series Analysis
- Final Project Presentations & Conclusion: Students present their final projects and course conclusion.
- Comprehensive exam covering all topics from the course.
Grading Policy
| Category | Percentage |
|---|---|
| Homework Assignments | 20% |
| Midterm Exam | 30% |
| Final Project | 20% |
| Final Exam | 30% |
Required Textbook
- Linear Algebra and Learning from Data by Gilbert Strang.
Recommended Readings
- Pattern Recognition and Machine Learning by Christopher Bishop.
- The Elements of Statistical Learning by Trevor Hastie, Robert Tibshirani, and Jerome Friedman.
Additional Information
- Academic Integrity Rules applicable to everyone.
- Contact Disability Services for special requests.
- Contact Information of Instructor provided, including office hours.
Teorema de Bayes
- The theorem describes the probability of an event based on prior knowledge of conditions related to the event.
- Basic Formula: $P(A|B) = \frac{P(B|A)P(A)}{P(B)}$
- $P(A|B)$: The conditional probability of A, given B is true.
- $P(B|A)$: The conditional probability of B, given A is true.
- $P(A)$ and $P(B)$: The probabilities of A and B being true independently.
Deducción del Teorema
- The theorem can be derived from basic definitions of conditional probability
- $P(A \cap B) = P(A|B)P(B) = P(B|A)P(A)$
- $P(A|B) = \frac{P(B|A)P(A)}{P(B)}$
Ejemplo
- A fictional test is 95% accurate when a person has disease A and 90% when a person does not have the disease.
- $P(A|B) = \frac{0.95 \cdot 0.01}{0.95 \cdot 0.01 + 0.10 \cdot 0.99} = 0.087$
- The probability the person has disease A is approximately 8.7%.
Studying That Suits You
Use AI to generate personalized quizzes and flashcards to suit your learning preferences.