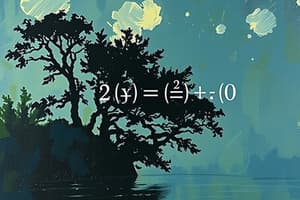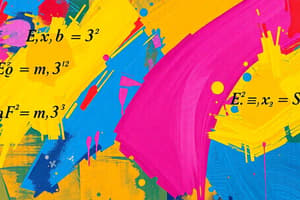Podcast
Questions and Answers
In the formula for the area of a rectangle, which variable is the subject of the formula?
In the formula for the area of a rectangle, which variable is the subject of the formula?
- b
- h
- A (correct)
- none of the above
In the formula A = bh, to isolate b, you need to add h to both sides.
In the formula A = bh, to isolate b, you need to add h to both sides.
False (B)
What is the inverse operation needed to remove +at from the equation v = u + at?
What is the inverse operation needed to remove +at from the equation v = u + at?
-at
To change the subject of a formula, you must ____ the variable to be isolated.
To change the subject of a formula, you must ____ the variable to be isolated.
Match the following formulas with their rearrangement to isolate the indicated variable:
Match the following formulas with their rearrangement to isolate the indicated variable:
Which formula can be rearranged to make k the subject?
Which formula can be rearranged to make k the subject?
The subject of a formula is always the variable that is alone on one side of the equals sign.
The subject of a formula is always the variable that is alone on one side of the equals sign.
The inverse operation of multiplying by h is ____ by h.
The inverse operation of multiplying by h is ____ by h.
Flashcards
Subject of a formula
Subject of a formula
The variable you're solving for in a formula.
Rearranging a formula
Rearranging a formula
Changing the subject of a formula to isolate another variable.
Inverse operations
Inverse operations
Opposite mathematical operations (addition/subtraction, multiplication/division).
Isolate a variable
Isolate a variable
Signup and view all the flashcards
Example: Finding 'b'
Example: Finding 'b'
Signup and view all the flashcards
Example: Finding 'u'
Example: Finding 'u'
Signup and view all the flashcards
Example: Finding 't'
Example: Finding 't'
Signup and view all the flashcards
Example: Finding 'k'
Example: Finding 'k'
Signup and view all the flashcards
Study Notes
Changing the Subject of a Formula
- A formula's subject is the variable you're solving for.
- It's the letter standing alone on one side of the equals sign.
- For example, in (A = bh), the subject is (A) (area).
Rearranging Formulas
- To change the subject, manipulate the formula to isolate the desired variable.
- Use inverse operations (like adding and subtracting, multiplying and dividing).
Example: Finding the Base of a Rectangle
- Given (A = bh), to find (b), divide both sides by (h):
- (b = \frac{A}{h})
- This isolates (b) and makes it the subject.
Example: Rearranging (v = u + at) to find (u)
- Subtract (at) from both sides to isolate (u):
- (u = v - at)
Example: Rearranging (v = u + at) to find (t)
- Subtract (u) from both sides: (v - u = at)
- Divide both sides by (a): (t = \frac{v - u}{a})
Example: Rearranging (P = \frac{k}{j}) to find (k)
- To isolate (k), multiply both sides by (j):
- (k = Pj)
Studying That Suits You
Use AI to generate personalized quizzes and flashcards to suit your learning preferences.