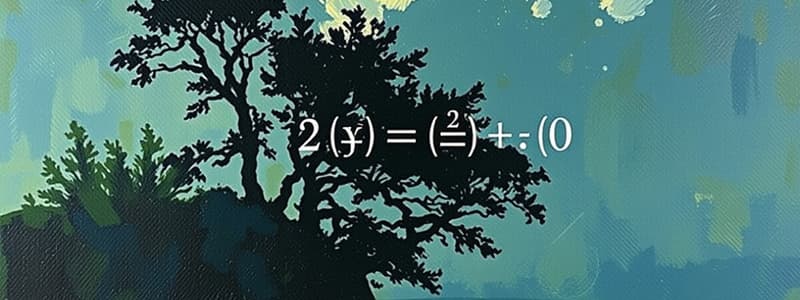Rearranging Equations Steps

Questions and Answers

What is the first step of rearranging formulas?

Get rid of any square root signs by squaring both sides.

What do you need to do next after getting rid of square root signs?

Get rid of fractions.

What do you do about brackets in an equation?

Multiply them out.

What do you do to the subject terms when rearranging equations?

Collect them all to one side and leave the non-subject terms on the other. Signup and view all the answers

What do you reduce the equation to?

The form Ax=B. Signup and view all the answers

What happens after you reduce the equation to the form Ax=B?

You divide both sides by A to give x=. Signup and view all the answers

If you are left with x², what do you do?

Square root both sides to give x=+/-. Signup and view all the answers

Make b the subject of the formula a=5b+3?

b=4a-3/5. Signup and view all the answers

Make u the subject of the formula v²=u²+2as?

u=+/-√(v²-2as). Signup and view all the answers

Make n the subject of the equation 2(m+3)=√n+3?

n=4m²+24m+31. Signup and view all the answers

Make p the subject of the formula q=p+1?

p=q+1/(q-1). Signup and view all the answers

Study Notes

Rearranging Equations Steps

Start by eliminating square roots by squaring both sides of the equation.
Remove any fractions present in the equation to simplify.
Expand and multiply out any brackets within the equation.
Consolidate all subject terms on one side while keeping non-subject terms on the opposite side.
The resulting form should be structured as Ax = B, with A representing coefficients of the variable and B representing constants.
Divide both sides by A to isolate the variable, resulting in the form x = (B/A).
If encountering x², take the square root of both sides to find x = ±√(expression).

Example: Making b the Subject of a Formula

For the equation a = 5b + 3, eliminate fractions by multiplying through by 4: 4a = 5b + 12.
Gather all subject terms (b terms) to one side to achieve: 5b = 4a - 12.
The equation is simplified to the form Ab = B, where A is 5 and B is the rearranged term.
Divide by 5 to solve for b, yielding b = (4a - 12)/5.

Example: Making u the Subject of a Formula

Given v² = u² + 2as, isolate u² by rearranging to u² = v² - 2as.
This leads to the form Au² = B.
To isolate u, take the square root of both sides resulting in: u = ±√(v² - 2as).

Example: Making n the Subject of a Formula

For the equation 2(m+3) = √n + 3, first square both sides to eliminate the square root: 4m² + 24m + 36 = n + 5.
Rearrange to isolate n, which gives n = 4m² + 24m + 31.

Example: Making p the Subject of a Formula

In the formula q = (p + 1)/(p - 1), first eliminate fractions by multiplying by (p - 1): q(p - 1).
Expand this to pq - q = p + 1.
Rearrange and consolidate terms to form pq - p = q + 1.
Factor similar terms leading to p(q - 1) = q + 1 and solve for p by dividing each side by (q - 1): p = (q + 1)/(q - 1).

Description

This quiz tests your understanding of the steps involved in rearranging equations to isolate a variable. It covers the elimination of square roots, removal of fractions, and other essential techniques needed to solve for a variable efficiently. Get ready to sharpen your algebra skills with practical examples!